Perfect Binary TreesThe ideal binary tree is a symbol of beauty, balance, and effectiveness in the large field of data structures and algorithms. Perfect binary trees, often referred to as full binary trees, are a fascinating subject that intrigues computer scientists, mathematicians, and nature lovers alike. They are a fascinating subject to study because of their symmetrical structure and recursive nature, and they have numerous uses in domains ranging from computer science to linguistics and beyond. In this thorough investigation, we will delve into the world of perfect binary trees and learn about their composition, characteristics, and wide range of uses. Understanding Perfect Binary TreesIt is crucial to understand the basic idea of a binary tree before we go into the intricate details of perfect binary trees. Each node in a binary tree, also known as the left and right children, can have a maximum of two children, making it a hierarchical data structure. A binary tree has zero, one, or two child nodes, and each node is made up of a value or key. Data storage, search algorithms, and a variety of other uses for binary trees are common in computer science and mathematics. 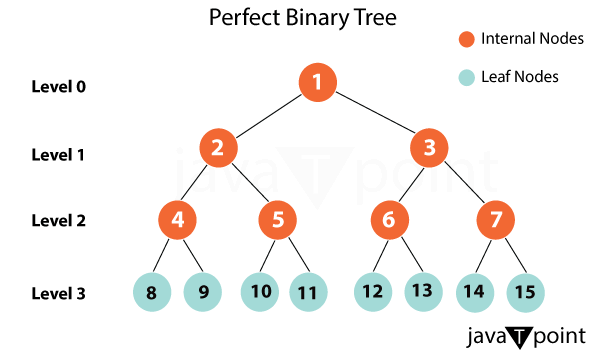
A particular variety of binary trees that displays an incredible degree of symmetry and balance is known as a perfect binary tree. Two essential requirements must be satisfied for a binary tree to be considered perfect:
The Ultimate SymmetryPerfect binary trees are distinguished from other binary tree versions by their inherent symmetry. Consider a perfect binary tree as a living illustration of the golden ratio, a beautiful and natural harmony. The tree appears to be a harmonious reflection of itself because the symmetric structure ensures that each node has left and right children. In addition to being visually appealing, perfect binary trees have considerable advantages in terms of time and space complexity for different algorithms and data structures. These trees' balanced structure optimizes search processes, making them accurate and efficient. This symmetrical trait forms the basis of various fundamental ideas and applications, and it offers a singular opportunity for investigating the realm of tree-based algorithms and data storage. Properties of Perfect Binary TreesPerfect binary trees display several characteristics that are both intriguing and useful in real-world applications. Let's examine some of these salient traits:
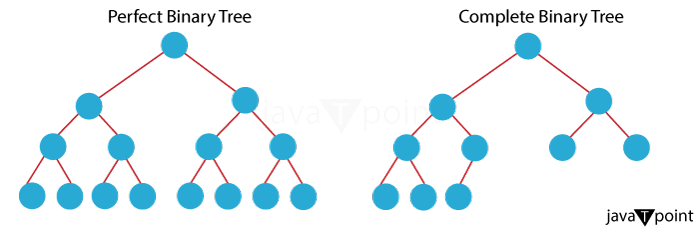
Applications of Perfect Binary TreesPerfect binary trees have many practical uses in a variety of fields, therefore their popularity extends beyond just the way they look and their theoretical characteristics. Here are a few notable uses for perfect binary trees:
Conclusion:With their symmetrical beauty and mathematical accuracy, perfect binary trees are more than just an interesting mystery. Numerous algorithms, data structures, and applications that drive the digital and computer world rely on them as their foundation. Perfect binary trees have symmetry and balance built in, which not only makes them beautiful to look at but also makes them useful for several optimization tasks. In Conclusion, perfect binary trees are more than just a theoretical idea; they represent the definition of beauty and effectiveness in the field of data structures. They serve as a reminder that the elegance of mathematics and computer science frequently coexist with usefulness and practical applications.
Next TopicReverse Sort
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share









