Huffman Tree in Data Structure
Introduction:
The Huffman tree, which bears the name of its inventor David A. Huffman, and was first introduced in 1952, is a key idea in the study of data structures and compression methods. Data compression has been revolutionized by the inventive binary tree structure, which is essential in shrinking the size of data while preserving its integrity. We shall delve into the complexities of Huffman trees in this article, looking at their design, uses, and importance in contemporary computing.
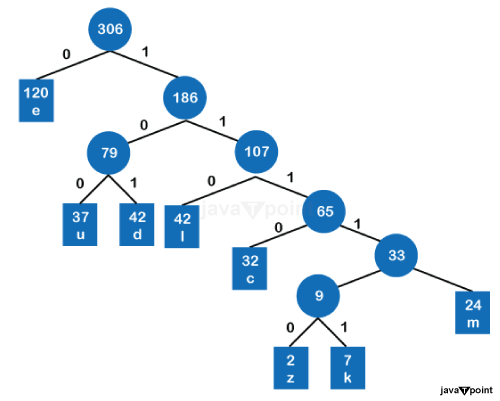
Restoration of Huffman Trees:
A Huffman tree is fundamentally a binary tree, where each leaf node stands for a distinct symbol in the input data, such as text characters in a document or image pixels. Assigning shorter codes to symbols that occur frequently and larger codes to those that do not frequently is the main concept behind the building of Huffman trees. The creation of Huffman codes, which starts this process, is accomplished by taking the following actions:
- Frequency Analysis: Analysing the frequency of each symbol in the incoming data is the first stage in creating a Huffman tree. By scanning the data and counting the instances of each sign, this can be accomplished.
- Symbol Sorting: Next, the symbols are arranged according to their frequency in ascending order. The more frequent symbols are evaluated first during tree formation thanks to this phase.
- Tree Building:The Huffman tree itself is built iteratively. Each symbol is first regarded as a single-node tree. The two trees with the lowest frequencies are then combined into one tree in a loop. The Huffman tree is the last tree standing after the progression described above.
- Code Assignment: As the Huffman tree is constructed, each symbol is given a code based on its location in the tree. A '0' is added to the code when moving left in the tree, and a '1' is added when traveling right. To ensure clear decoding, these codes are created so that no code is the prefix of another.
Applications of Huffman Trees:
Due to its effective data compression capabilities, Huffman trees are widely used in many different fields. Huffman trees are famously employed in places like:
- Data Compression: In data compression methods like ZIP and GZIP, Huffman coding is frequently used. These algorithms greatly reduce the quantity of the input data while enabling lossless decompression by swapping out symbols for their equivalent Huffman codes.
- Image Compression: Huffman trees are used to effectively compress picture data in image compression algorithms like JPEG. The coefficients generated after Discrete Cosine Transform (DCT) are then subjected to Huffman coding in JPEG compression.
- Text Compression: The use of Huffman coding helps to make text files smaller. Huffman trees are used in text compression programs like LZW (used in GIF) and DEFLATE (used in PNG) to increase compression ratios.
- Network communication: To conserve bandwidth, Huffman coding is used in data transmission through networks. It is essential for web-based applications and multimedia streaming because it enables speedier data transfer.
Significance of Huffman Trees:
It is impossible to overestimate the importance of Huffman trees in data structures and computer science. The following major points highlight their significance:
- Space Efficient: By assigning shorter codes to frequently recurring symbols, Huffman trees excel at data compression. As a result, data is stored and sent more effectively, which is important in contemporary computing systems.
- Fast Decoding: Data encoded using the Huffman encoding can be decoded incredibly quickly thanks to the binary tree structure. Each byte in the encoded data determines the path to take as the tree is traversed from the root to a leaf node.
- Universality: Huffman coding is a universal method for data compression since it is flexible and may be used with many types of data.
- Algorithmic Foundation: Huffman tree creation gives programmers and computer scientists a fundamental understanding of tree-based data structures and algorithms.
Conclusion:
The Huffman tree is a masterwork of data organization and compression, to sum up. It is a cornerstone of contemporary computing because of its beautiful design and effective encoding. Huffman trees have made it possible to compress and transport data with little information loss by giving shorter codes to frequently recurring symbols. Huffman trees' significance in data compression is unwavering even as technology develops, providing effective information storage, transmission, and retrieval in the digital age.
|

 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now









