Minimum Possible value of |ai + aj - k| for given array and k
Introduction
In the realm of computer science and mathematics, optimization problems are a common thread that weaves through various fields. One such intriguing problem is finding the minimum possible value of the expression |ai + aj - k|, where ai and aj are distinct elements from a given array, and k is a constant. This problem holds significance in algorithm design, data manipulation, and various real-world applications.
Understanding the Problem
Given an array of integers and a constant value k, the objective is to identify the pair of distinct array elements that minimizes the absolute difference between their sum and k. Mathematically, we aim to find the values of ai and aj that minimize the expression |ai + aj - k|.
Formally, the problem can be stated as follows:
Given an array A of size n and an integer k, find distinct indices i and j (1 ≤ i, j ≤ n, i ≠ j) such that |A[i] + A[j] - k| is minimized.
Illustration with Example
Let's illustrate this problem with an example to enhance our understanding. Consider the following array:
Array A: [3, 8, 10, 15, 20]
Constant k: 17
We need to find two distinct elements from the array whose sum is closest to the constant k. In this case, the values 8 and 10 have a sum of 18, which is closest to 17 among all possible pairs. The absolute difference |8 + 10 - 17| equals 1, which is the minimum possible value for this example.
Approach and Algorithm
To solve this problem efficiently, we need to consider some key insights:
- Sorting: One crucial step is to sort the given array in ascending order. Sorting the array enables us to make informed decisions while traversing through the elements.
- Two-Pointer Technique: After sorting the array, we can utilize the two-pointer technique. We initialize two pointers, one at the beginning of the array and the other at the end. These pointers will gradually move towards each other.
- Finding the Minimum Value: As the pointers move towards each other, we calculate the absolute difference between the sum of the elements pointed to by the two pointers and the target value k. We keep track of the minimum absolute difference encountered during this traversal.
- Updating Pointers: Depending on the current calculated difference, we update the pointers. If the sum is less than k, we increment the left pointer to consider a larger element. If the sum is greater than k, we decrement the right pointer to consider a smaller element.
- Termination: We continue this process until the two pointers meet or cross each other. At this point, we will have explored all possible pairs, and we can conclude with the minimum possible value of |ai + aj - k|.
Significance of the Problem
The problem of finding the minimum possible value of |ai + aj - k| has practical implications in various domains. It is a fundamental component in data analysis, where the goal is to discover meaningful patterns or relationships within datasets. This problem can help identify pairs of values in a dataset that exhibit a certain level of closeness to a given target value, contributing to anomaly detection or clustering applications.
Furthermore, this problem has relevance in optimization scenarios. Consider scenarios where resources need to be allocated optimally, and the goal is to minimize the difference between available resources and the desired target (represented by k). Solving this problem aids in making decisions that lead to more balanced and efficient resource allocation.
Problem Statement
Given an array of integers and a constant value 'k', the task is to find the minimum possible value of the expression |ai + aj - k|, where ai and aj are two distinct elements from the array.
Naive Approach
A naive approach to solving this problem involves considering all pairs of elements from the array and calculating the expression for each pair. We can then keep track of the minimum value encountered. However, this approach has a time complexity of O(n^2), which becomes inefficient for larger arrays.
Explanation:
- The function minAbsDiff takes three parameters: an integer array arr, its size n, and an integer k.
- This function is responsible for finding the pair of elements in the array whose sum is closest to k, and returning the absolute difference between their sum and k.
- Inside the minAbsDiff function, the variable minDiff is initialized to a large value Then, the program uses nested loops to iterate through all possible pairs of elements in the array.
- For each pair, it calculates the absolute difference between their sum and k, and updates the minDiff if the calculated difference is smaller than the current
- The main function is where the user is prompted to input the size of the array, followed by the array elements, and finally the value of k.
- After obtaining the inputs, it calls the minAbsDiff function and stores the result. Finally, the program outputs the minimum possible value of the absolute difference between the sum of a pair of array elements and k.
Program Output:
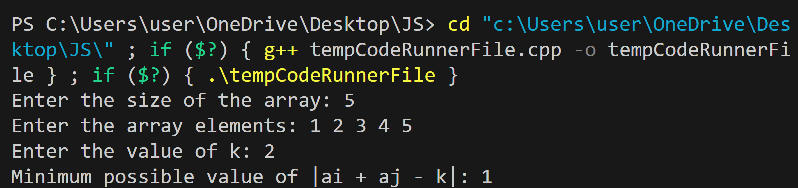
Optimized Approach
To solve this problem more efficiently, we can utilize a two-pointer approach. The idea is to sort the array and then initialize two pointers, one pointing to the beginning and the other pointing to the end of the sorted array. We can then calculate the expression for the sum of the elements pointed to by the two pointers and update the minimum difference accordingly. Depending on whether the sum is greater or smaller than 'k', we can adjust the pointers to move towards each other.
This optimized approach has a time complexity of O(n log n) due to the sorting step.
Explanation:
- The core function of the program is minAbsDiff, which has three parameters: an integer array arr, its size n, and an integer
- This function employs a two-pointer approach to find the pair of elements that provides the minimum absolute difference between their sum and the target k.
- Within the minAbsDiff function, the array arr is sorted in ascending order using the sort function from the C++ standard library. Two pointers, left and right, are initialized to the start and end of the sorted array, respectively. Additionally, the variable minDiff is initialized to a large value INT_MAX.
- The program then enters a loop that continues as long as the left pointer is less than the right In each iteration, it calculates the sum of the elements pointed to by the left and right pointers.
- It then computes the absolute difference between this sum and the target value k.
- The calculated absolute difference is compared to the current minDiff, and if it is smaller, minDiff is updated with the new value. This step ensures that the program keeps track of the minimum absolute difference found so far.
- Depending on the comparison between the sum and k, the program either increments the left pointer (if the sum is less than k) or decrements the right pointer (if the sum is greater than or equal to k).
- This approach is employed to explore pairs of elements that might result in a sum closer to the target k.
- Once the pointers meet or cross each other, the loop stops, and the function returns the calculated minimum absolute difference.
- In the main function, the user is prompted to input the size of the array, followed by the array elements.
- Then, the target value k is taken as input. The program subsequently calls the minAbsDiff function and stores the result, which represents the minimum possible value of the absolute difference between the sum of a pair of array elements and the target value k. Finally, this result is displayed to the user.
Program Output:
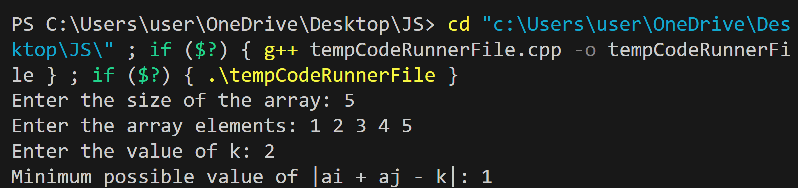
Real-World Use Cases
The problem of finding the minimum possible value of |ai + aj - k| has a wide range of applications across diverse fields:
- Financial Analysis: In finance, this problem can help identify pairs of stock prices that exhibit a combined movement closest to a desired target. This can be useful in pairs trading and portfolio management.
- Image Processing: In image processing, the problem can be applied to pixel intensity analysis. Given a target intensity level, the algorithm can identify pairs of pixels that, when combined, create an intensity closest to the target.
- Resource Allocation: When allocating resources in supply chain management or production planning, this problem can assist in optimizing the allocation to minimize deviations from the desired total.
- Sensor Networks: In sensor networks, such as environmental monitoring systems, the problem can aid in identifying pairs of sensor readings that are closest to a specified threshold.
Advanced Techniques and Optimizations
While the brute-force and two-pointer approaches are fundamental methods to solve the problem, there are additional techniques and optimizations that can further enhance the efficiency of finding the minimum possible value of |ai + aj - k|.
- Using Binary Search: If the array is sorted, binary search can be employed to find the element closest to k - ai in the array. This reduces the search time to logarithmic complexity. The overall time complexity becomes O(n log n) due to the initial sorting step and the binary search.
- Using Data Structures: Utilizing data structures like heaps or priority queues can help efficiently manage the process of finding the closest value to k - ai in the array. This can be particularly beneficial when dealing with large datasets.
- Optimal Index Pairing: For arrays with distinct elements, sorting the array and then using the two-pointer approach guarantees finding the optimal pair. However, if the array has duplicate elements, additional considerations are needed to ensure the optimal pair is selected.
- Divide and Conquer: An advanced approach involves dividing the array into smaller subproblems and solving them recursively. This technique can be effective when combined with certain data structures and sorting algorithms.
Conclusion
In conclusion, the problem of determining the minimum possible value of the expression |ai + aj - k| for a given array and constant 'k' can be effectively tackled through algorithmic strategies. While a naive approach involves considering all pairs of elements and calculating the expression for each pair, an optimized approach takes advantage of sorting and a two-pointer technique to significantly improve efficiency.
The optimized approach, with a time complexity of O(n log n) due to the sorting step, demonstrates the power of algorithmic optimization in solving challenges related to array manipulation. By sorting the array and intelligently adjusting pointers based on the comparison of element sums with 'k', the algorithm arrives at the minimum absolute difference efficiently.
This technique not only showcases the importance of algorithmic thinking in competitive programming but also emphasizes the value of leveraging optimized solutions to tackle complex problems in a time-efficient manner. Aspiring programmers can enhance their problem-solving skills by mastering such techniques, enabling them to confidently address a wide array of algorithmic challenges.
|


 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now









