Counting Sort Algorithm

In this article, we will discuss the counting sort Algorithm. Counting sort is a sorting technique that is based on the keys between specific ranges. In coding or technical interviews for software engineers, sorting algorithms are widely asked. So, it is important to discuss the topic.

This sorting technique doesn't perform sorting by comparing elements. It performs sorting by counting objects having distinct key values like hashing. After that, it performs some arithmetic operations to calculate each object's index position in the output sequence. Counting sort is not used as a general-purpose sorting algorithm.

Counting sort is effective when range is not greater than number of objects to be sorted. It can be used to sort the negative input values.

Now, let's see the algorithm of counting sort.

Algorithm

countingSort(array, n) // 'n' is the size of array
max = find maximum element in the given array
create count array with size maximum + 1
Initialize count array with all 0's
for i = 0 to n
find the count of every unique element and 
store that count at ith position in the count array
for j = 1 to max
Now, find the cumulative sum and store it in count array
for i = n to 1
Restore the array elements
Decrease the count of every restored element by 1
end countingSort

Working of counting sort Algorithm

Now, let's see the working of the counting sort Algorithm.

To understand the working of the counting sort algorithm, let's take an unsorted array. It will be easier to understand the counting sort via an example.

Let the elements of array are -

1. Find the maximum element from the given array. Let max be the maximum element.

2. Now, initialize array of length max + 1 having all 0 elements. This array will be used to store the count of the elements in the given array.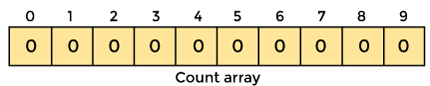

3. Now, we have to store the count of each array element at their corresponding index in the count array.

The count of an element will be stored as - Suppose array element '4' is appeared two times, so the count of element 4 is 2. Hence, 2 is stored at the 4^th position of the count array. If any element is not present in the array, place 0, i.e. suppose element '3' is not present in the array, so, 0 will be stored at 3^rd position.

Now, store the cumulative sum of count array elements. It will help to place the elements at the correct index of the sorted array.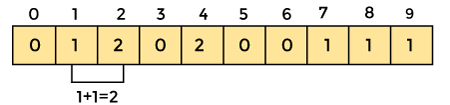

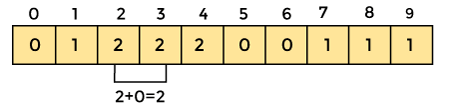
Similarly, the cumulative count of the count array is -

4. Now, find the index of each element of the original array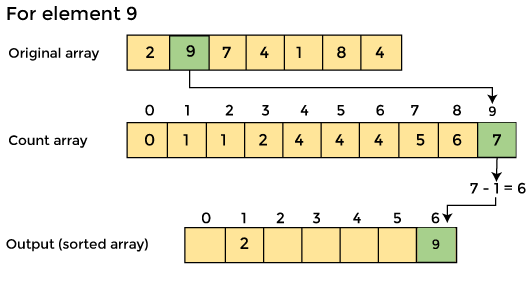

After placing element at its place, decrease its count by one. Before placing element 2, its count was 2, but after placing it at its correct position, the new count for element 2 is 1.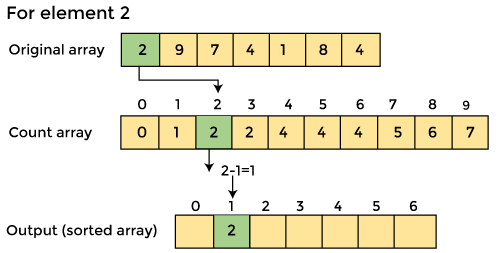

Similarly, after sorting, the array elements are -

Now, the array is completely sorted.

Counting sort complexity

Now, let's see the time complexity of counting sort in best case, average case, and in worst case. We will also see the space complexity of the counting sort.

1. Time Complexity

Case	Time	Complexity
Best Case	O(n + k)
Average Case	O(n + k)
Worst Case	O(n + k)

Best Case Complexity - It occurs when there is no sorting required, i.e. the array is already sorted. The best-case time complexity of counting sort is O(n + k).
Average Case Complexity - It occurs when the array elements are in jumbled order that is not properly ascending and not properly descending. The average case time complexity of counting sort is O(n + k).
Worst Case Complexity - It occurs when the array elements are required to be sorted in reverse order. That means suppose you have to sort the array elements in ascending order, but its elements are in descending order. The worst-case time complexity of counting sort is O(n + k).

In all above cases, the time complexity of counting sort is same. This is because the algorithm goes through n+k times, regardless of how the elements are placed in the array.

Counting sort is better than the comparison-based sorting techniques because there is no comparison between elements in counting sort. But, when the integers are very large the counting sort is bad because arrays of that size have to be created.

2. Space Complexity

Space Complexity	O(max)
Stable	YES

The space complexity of counting sort is O(max). The larger the range of elements, the larger the space complexity.

Implementation of counting sort

Now, let's see the programs of counting sort in different programming languages.

Program: Write a program to implement counting sort in C language.

#include<stdio.h>

int getMax(int a[], int n) {
   int max = a[0];
   for(int i = 1; i<n; i++) {
      if(a[i] > max)
         max = a[i];
   }
   return max; //maximum element from the array
}

void countSort(int a[], int n) // function to perform counting sort
{
   int output[n+1];
   int max = getMax(a, n);
   int count[max+1]; //create count array with size [max+1]


  for (int i = 0; i <= max; ++i) 
  {
    count[i] = 0; // Initialize count array with all zeros
  }
  
  for (int i = 0; i < n; i++) // Store the count of each element
  {
    count[a[i]]++;
  }

   for(int i = 1; i<=max; i++) 
      count[i] += count[i-1]; //find cumulative frequency

  /* This loop will find the index of each element of the original array in count array, and
   place the elements in output array*/
  for (int i = n - 1; i >= 0; i--) {
    output[count[a[i]] - 1] = a[i];
    count[a[i]]--; // decrease count for same numbers
}

   for(int i = 0; i<n; i++) {
      a[i] = output[i]; //store the sorted elements into main array
   }
}

void printArr(int a[], int n) /* function to print the array */
{
	int i;
	for (i = 0; i < n; i++)
		printf("%d ", a[i]);
}

int main() {
   	int a[] = { 11, 30, 24, 7, 31, 16 };
   	int n = sizeof(a)/sizeof(a[0]);
    printf("Before sorting array elements are - \n");
    printArr(a, n);
    countSort(a, n);
    printf("\nAfter sorting array elements are - \n");  
    printArr(a, n);
	return 0;

}

Output

After the execution of above code, the output will be -

Program: Write a program to implement counting sort in C++.

#include <iostream>

using namespace std;

int getMax(int a[], int n) {
   int max = a[0];
   for(int i = 1; i<n; i++) {
      if(a[i] > max)
         max = a[i];
   }
   return max; //maximum element from the array
}

void countSort(int a[], int n) // function to perform counting sort
{
   int output[n+1];
   int max = getMax(a, n);
   int count[max+1]; //create count array with size [max+1]


  for (int i = 0; i <= max; ++i) 
  {
    count[i] = 0; // Initialize count array with all zeros
  }
  
  for (int i = 0; i < n; i++) // Store the count of each element
  {
    count[a[i]]++;
  }

   for(int i = 1; i<=max; i++) 
      count[i] += count[i-1]; //find cumulative frequency

  /* This loop will find the index of each element of the original array in count array, and
   place the elements in output array*/
  for (int i = n - 1; i >= 0; i--) {
    output[count[a[i]] - 1] = a[i];
    count[a[i]]--; // decrease count for same numbers
}

   for(int i = 0; i<n; i++) {
      a[i] = output[i]; //store the sorted elements into main array
   }
}

void printArr(int a[], int n) /* function to print the array */
{
	int i;
	for (i = 0; i < n; i++)
		cout<<a[i]<<" ";
}

int main() {
   	int a[] = { 31, 11, 42, 7, 30, 11 };
   	int n = sizeof(a)/sizeof(a[0]);
    cout<<"Before sorting array elements are - \n";
    printArr(a, n);
    countSort(a, n);
    cout<<"\nAfter sorting array elements are - \n";  
    printArr(a, n);
	return 0;
}

Output

After the execution of above code, the output will be -

Program: Write a program to implement counting sort in C#.

using System;
class CountingSort {

static int getMax(int[] a, int n) {
  int max = a[0];
  for(int i = 1; i<n; i++) {
      if(a[i] > max)
         max = a[i];
  }
  return max; //maximum element from the array
}

static void countSort(int[] a, int n) // function to perform counting sort
{
   int[] output = new int [n+1];
   int max = getMax(a, n);
   int[] count = new int [max+1]; //create count array with size [max+1]

  for (int i = 0; i <= max; ++i) 
  {
    count[i] = 0; // Initialize count array with all zeros
  }
  
  for (int i = 0; i < n; i++) // Store the count of each element
  {
    count[a[i]]++;
  }

   for(int i = 1; i<=max; i++) 
      count[i] += count[i-1]; //find cumulative frequency

  /* This loop will find the index of each element of the original array in count array, and
   place the elements in output array*/
  for (int i = n - 1; i >= 0; i--) {
    output[count[a[i]] - 1] = a[i];
    count[a[i]]--; // decrease count for same numbers
}

   for(int i = 0; i<n; i++) {
      a[i] = output[i]; //store the sorted elements into main array
   }
}

static void printArr(int[] a, int n) /* function to print the array */
{
	int i;
	for (i = 0; i < n; i++)
		Console.Write(a[i] + " ");
}

  static void Main() {
   	int[] a = { 43, 31, 2, 7, 10, 1, 5, 6, 3 };
   	int n = a.Length;
    Console.Write("Before sorting array elements are - \n");
    printArr(a,n);
    countSort(a,n);
    Console.Write("\nAfter sorting array elements are - \n");  
    printArr(a,n);
}
}

Output

After the execution of above code, the output will be -

Program: Write a program to implement counting sort in Java.

class CountingSort {

int getMax(int[] a, int n) {
  int max = a[0];
  for(int i = 1; i<n; i++) {
      if(a[i] > max)
         max = a[i];
  }
  return max; //maximum element from the array
}

void countSort(int[] a, int n) // function to perform counting sort
{
   int[] output = new int [n+1];
   int max = getMax(a, n);
   //int max = 42;
   int[] count = new int [max+1]; //create count array with size [max+1]

  for (int i = 0; i <= max; ++i) 
  {
    count[i] = 0; // Initialize count array with all zeros
  }
  
  for (int i = 0; i < n; i++) // Store the count of each element
  {
    count[a[i]]++;
  }

   for(int i = 1; i<=max; i++) 
      count[i] += count[i-1]; //find cumulative frequency

  /* This loop will find the index of each element of the original array in 

count array, and
   place the elements in output array*/
  for (int i = n - 1; i >= 0; i--) {
    output[count[a[i]] - 1] = a[i];
    count[a[i]]--; // decrease count for same numbers
}

   for(int i = 0; i<n; i++) {
      a[i] = output[i]; //store the sorted elements into main array
   }
}

/* Function to print the array elements */
void printArray(int a[], int n)
{
	int i;
	for (i = 0; i < n; i++)
		System.out.print(a[i] + " ");
}

public static void main(String args[])
{
	int a[] = { 11, 30, 24, 7, 31, 16, 39, 41 };
	int n = a.length;
	CountingSort c1 = new CountingSort();
    System.out.println("\nBefore sorting array elements are - ");
	c1.printArray(a, n);
	c1.countSort(a,n);
    System.out.println("\nAfter sorting array elements are - ");
	c1.printArray(a, n);
    System.out.println();
}
}

Output

Program: Write a program to implement counting sort in PHP.

<?php

function getMax($a, $n) {
  $max = $a[0];
  for($i = 1; $i < $n; $i++) {
      if($a[$i] > $max)
         $max = $a[$i];
  }
  return $max; //maximum element from the array
}

function countSort(&$a, $n) // function to perform counting sort
{
    $LeftArray = array($n + 1);
   $max = getMax($a, $n);
   $count = array($max + 1); //create count array with size [max+1]

  for ($i = 0; $i <= $max; ++$i) 
  {
    $count[$i] = 0; // Initialize count array with all zeros
  }
  
  for ($i = 0; $i < $n; $i++) // Store the count of each element
  {
    $count[$a[$i]]++;
  }

   for($i = 1; $i<=$max; $i++) 
      $count[$i] += $count[$i-1]; //find cumulative frequency

  /* This loop will find the index of each element of the original array in  
count array, and
   place the elements in output array*/
  for ($i = $n - 1; $i >= 0; $i--) {
    $output[$count[$a[$i]] - 1] = $a[$i];
    $count[$a[$i]]--; // decrease count for same numbers
}

   for($i = 0; $i<$n; $i++) {
      $a[$i] = $output[$i]; //store the sorted elements into main array
   }
}

/* Function to print the array elements */
function printArray($a, $n)
{
    for($i = 0; $i < $n; $i++)  
    {  
        print_r($a[$i]);  
        echo " ";  
    }      
}

	$a = array( 9, 28, 22, 5, 29, 14, 37, 28, 9 );  
	$n = count($a);
    echo "Before sorting array elements are - <br>";  
    printArray($a, $n);
	countSort($a,$n);
    echo "<br> After sorting array elements are - <br>";  
    printArray($a, $n);

?>

Output

So, that's all about the article. Hope the article will be helpful and informative to you.

This article was not only limited to the algorithm. We have also discussed counting sort complexity, working, and implementation in different programming languages.

Next TopicHeap Sort

← prev next →