Tree Data Structure

We read the linear data structures like an array, linked list, stack and queue in which all the elements are arranged in a sequential manner. The different data structures are used for different kinds of data.

Some factors are considered for choosing the data structure:

• What type of data needs to be stored?: It might be a possibility that a certain data structure can be the best fit for some kind of data.
• Cost of operations: If we want to minimize the cost for the operations for the most frequently performed operations. For example, we have a simple list on which we have to perform the search operation; then, we can create an array in which elements are stored in sorted order to perform the binary search. The binary search works very fast for the simple list as it divides the search space into half.
• Memory usage: Sometimes, we want a data structure that utilizes less memory.

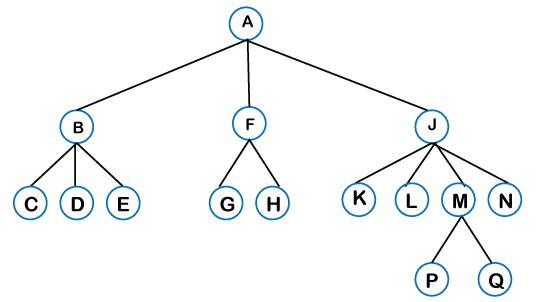
A tree is also one of the data structures that represent hierarchical data. Suppose we want to show the employees and their positions in the hierarchical form then it can be represented as shown below: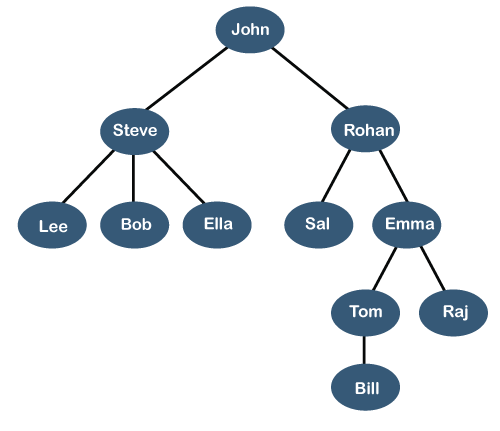

The above tree shows the organization hierarchy of some company. In the above structure, john is the CEO of the company, and John has two direct reports named as Steve and Rohan. Steve has three direct reports named Lee, Bob, Ella where Steve is a manager. Bob has two direct reports named Sal and Emma. Emma has two direct reports named Tom and Raj. Tom has one direct report named Bill. This particular logical structure is known as a Tree. Its structure is similar to the real tree, so it is named a Tree. In this structure, the root is at the top, and its branches are moving in a downward direction. Therefore, we can say that the Tree data structure is an efficient way of storing the data in a hierarchical way.

Let's understand some key points of the Tree data structure.

• A tree data structure is defined as a collection of objects or entities known as nodes that are linked together to represent or simulate hierarchy.
• A tree data structure is a non-linear data structure because it does not store in a sequential manner. It is a hierarchical structure as elements in a Tree are arranged in multiple levels.
• In the Tree data structure, the topmost node is known as a root node. Each node contains some data, and data can be of any type. In the above tree structure, the node contains the name of the employee, so the type of data would be a string.
• Each node contains some data and the link or reference of other nodes that can be called children.

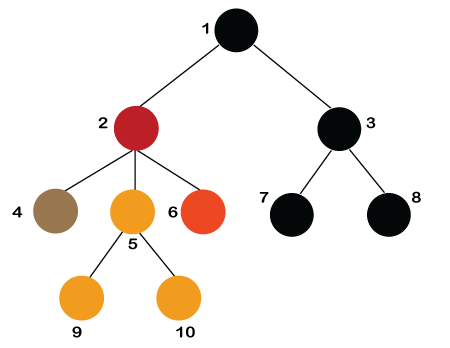
Some basic terms used in Tree data structure.

Let's consider the tree structure, which is shown below: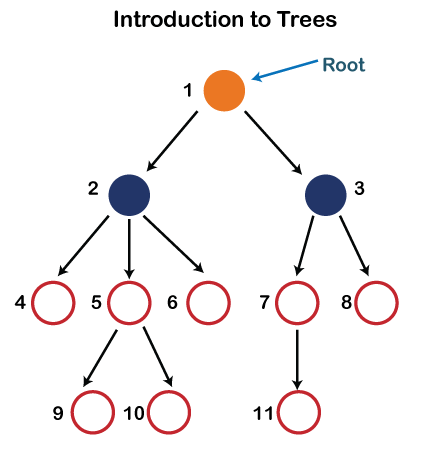

In the above structure, each node is labeled with some number. Each arrow shown in the above figure is known as a link between the two nodes.

• Root: The root node is the topmost node in the tree hierarchy. In other words, the root node is the one that doesn't have any parent. In the above structure, node numbered 1 is the root node of the tree. If a node is directly linked to some other node, it would be called a parent-child relationship.
• Child node: If the node is a descendant of any node, then the node is known as a child node.
• Parent: If the node contains any sub-node, then that node is said to be the parent of that sub-node.
• Sibling: The nodes that have the same parent are known as siblings.
• Leaf Node:- The node of the tree, which doesn't have any child node, is called a leaf node. A leaf node is the bottom-most node of the tree. There can be any number of leaf nodes present in a general tree. Leaf nodes can also be called external nodes.
• Internal nodes: A node has atleast one child node known as an internal
• Ancestor node:- An ancestor of a node is any predecessor node on a path from the root to that node. The root node doesn't have any ancestors. In the tree shown in the above image, nodes 1, 2, and 5 are the ancestors of node 10.
• Descendant: The immediate successor of the given node is known as a descendant of a node. In the above figure, 10 is the descendant of node 5.

Properties of Tree data structure

• Recursive data structure: The tree is also known as a recursive data structure. A tree can be defined as recursively because the distinguished node in a tree data structure is known as a root node. The root node of the tree contains a link to all the roots of its subtrees. The left subtree is shown in the yellow color in the below figure, and the right subtree is shown in the red color. The left subtree can be further split into subtrees shown in three different colors. Recursion means reducing something in a self-similar manner. So, this recursive property of the tree data structure is implemented in various applications.
  
• Number of edges: If there are n nodes, then there would n-1 edges. Each arrow in the structure represents the link or path. Each node, except the root node, will have atleast one incoming link known as an edge. There would be one link for the parent-child relationship.
• Depth of node x: The depth of node x can be defined as the length of the path from the root to the node x. One edge contributes one-unit length in the path. So, the depth of node x can also be defined as the number of edges between the root node and the node x. The root node has 0 depth.
• Height of node x: The height of node x can be defined as the longest path from the node x to the leaf node.

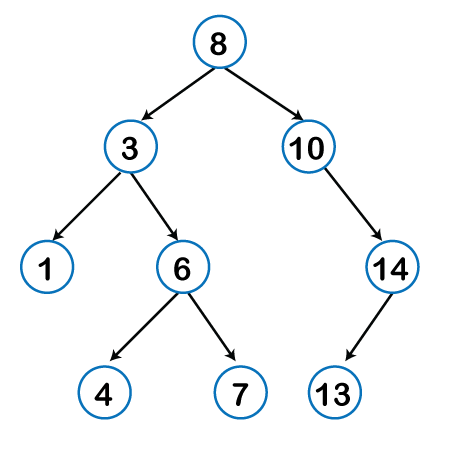
Based on the properties of the Tree data structure, trees are classified into various categories.

Implementation of Tree

The tree data structure can be created by creating the nodes dynamically with the help of the pointers. The tree in the memory can be represented as shown below: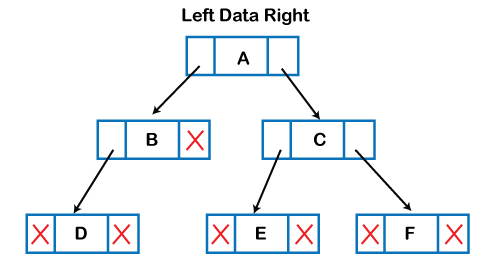

The above figure shows the representation of the tree data structure in the memory. In the above structure, the node contains three fields. The second field stores the data; the first field stores the address of the left child, and the third field stores the address of the right child.

In programming, the structure of a node can be defined as:

The above structure can only be defined for the binary trees because the binary tree can have utmost two children, and generic trees can have more than two children. The structure of the node for generic trees would be different as compared to the binary tree.

Applications of trees

The following are the applications of trees:

• Storing naturally hierarchical data: Trees are used to store the data in the hierarchical structure. For example, the file system. The file system stored on the disc drive, the file and folder are in the form of the naturally hierarchical data and stored in the form of trees.
• Organize data: It is used to organize data for efficient insertion, deletion and searching. For example, a binary tree has a logN time for searching an element.
• Trie: It is a special kind of tree that is used to store the dictionary. It is a fast and efficient way for dynamic spell checking.
• Heap: It is also a tree data structure implemented using arrays. It is used to implement priority queues.
• B-Tree and B+Tree: B-Tree and B+Tree are the tree data structures used to implement indexing in databases.
• Routing table: The tree data structure is also used to store the data in routing tables in the routers.

Types of Tree data structure

The following are the types of a tree data structure:

• General tree: The general tree is one of the types of tree data structure. In the general tree, a node can have either 0 or maximum n number of nodes. There is no restriction imposed on the degree of the node (the number of nodes that a node can contain). The topmost node in a general tree is known as a root node. The children of the parent node are known as subtrees.
  
  There can be n number of subtrees in a general tree. In the general tree, the subtrees are unordered as the nodes in the subtree cannot be ordered.
  Every non-empty tree has a downward edge, and these edges are connected to the nodes known as child nodes. The root node is labeled with level 0. The nodes that have the same parent are known as siblings.
• Binary tree: Here, binary name itself suggests two numbers, i.e., 0 and 1. In a binary tree, each node in a tree can have utmost two child nodes. Here, utmost means whether the node has 0 nodes, 1 node or 2 nodes.
  
  To know more about the binary tree, click on the link given below:
  https://www.javatpoint.com/binary-tree
• Binary Search tree: Binary search tree is a non-linear data structure in which one node is connected to n number of nodes. It is a node-based data structure. A node can be represented in a binary search tree with three fields, i.e., data part, left-child, and right-child. A node can be connected to the utmost two child nodes in a binary search tree, so the node contains two pointers (left child and right child pointer).
  Every node in the left subtree must contain a value less than the value of the root node, and the value of each node in the right subtree must be bigger than the value of the root node.

A node can be created with the help of a user-defined data type known as struct, as shown below:

The above is the node structure with three fields: data field, the second field is the left pointer of the node type, and the third field is the right pointer of the node type.

To know more about the binary search tree, click on the link given below:

https://www.javatpoint.com/binary-search-tree

• AVL tree

It is one of the types of the binary tree, or we can say that it is a variant of the binary search tree. AVL tree satisfies the property of the binary tree as well as of the binary search tree. It is a self-balancing binary search tree that was invented by Adelson Velsky Lindas. Here, self-balancing means that balancing the heights of left subtree and right subtree. This balancing is measured in terms of the balancing factor.

We can consider a tree as an AVL tree if the tree obeys the binary search tree as well as a balancing factor. The balancing factor can be defined as the difference between the height of the left subtree and the height of the right subtree. The balancing factor's value must be either 0, -1, or 1; therefore, each node in the AVL tree should have the value of the balancing factor either as 0, -1, or 1.

To know more about the AVL tree, click on the link given below:

https://www.javatpoint.com/avl-tree

• Red-Black Tree

The red-Black tree is the binary search tree. The prerequisite of the Red-Black tree is that we should know about the binary search tree. In a binary search tree, the value of the left-subtree should be less than the value of that node, and the value of the right-subtree should be greater than the value of that node. As we know that the time complexity of binary search in the average case is log₂n, the best case is O(1), and the worst case is O(n).

When any operation is performed on the tree, we want our tree to be balanced so that all the operations like searching, insertion, deletion, etc., take less time, and all these operations will have the time complexity of log₂n.

The red-black tree is a self-balancing binary search tree. AVL tree is also a height balancing binary search tree then why do we require a Red-Black tree. In the AVL tree, we do not know how many rotations would be required to balance the tree, but in the Red-black tree, a maximum of 2 rotations are required to balance the tree. It contains one extra bit that represents either the red or black color of a node to ensure the balancing of the tree.

• Splay tree

The splay tree data structure is also binary search tree in which recently accessed element is placed at the root position of tree by performing some rotation operations. Here, splaying means the recently accessed node. It is a self-balancing binary search tree having no explicit balance condition like AVL tree.

It might be a possibility that height of the splay tree is not balanced, i.e., height of both left and right subtrees may differ, but the operations in splay tree takes order of logN time where n is the number of nodes.

Splay tree is a balanced tree but it cannot be considered as a height balanced tree because after each operation, rotation is performed which leads to a balanced tree.

• Treap

Treap data structure came from the Tree and Heap data structure. So, it comprises the properties of both Tree and Heap data structures. In Binary search tree, each node on the left subtree must be equal or less than the value of the root node and each node on the right subtree must be equal or greater than the value of the root node. In heap data structure, both right and left subtrees contain larger keys than the root; therefore, we can say that the root node contains the lowest value.

In treap data structure, each node has both key and priority where key is derived from the Binary search tree and priority is derived from the heap data structure.

The Treap data structure follows two properties which are given below:

• Right child of a node>=current node and left child of a node <=current node (binary tree)
• Children of any subtree must be greater than the node (heap)

• B-tree

B-tree is a balanced m-way tree where m defines the order of the tree. Till now, we read that the node contains only one key but b-tree can have more than one key, and more than 2 children. It always maintains the sorted data. In binary tree, it is possible that leaf nodes can be at different levels, but in b-tree, all the leaf nodes must be at the same level.

If order is m then node has the following properties:

• Each node in a b-tree can have maximum m children
• For minimum children, a leaf node has 0 children, root node has minimum 2 children and internal node has minimum ceiling of m/2 children. For example, the value of m is 5 which means that a node can have 5 children and internal nodes can contain maximum 3 children.
• Each node has maximum (m-1) keys.

The root node must contain minimum 1 key and all other nodes must contain atleast ceiling of m/2 minus 1 keys.