Find Triplets with zero-sum

Consider a situation in which various unique components are given as a puzzle. This array has a hidden pattern: triplets with a zero sum. The objective is to crack this protected code, locate these illusive triplets, and in a concise manner present them. The mathematical goal is to identify every distinct triplet (a, b, c) in the array such that a + b + c = 0.

Given an array of distinct elements. The task is to find triplets in the array whose sum is zero.

Examples :

Input: arr[] = {0, -1, 2, -3, 1}

Output: (0 -1 1), (2 -3 1)

Explanation: The triplets with zero sum are 0 + -1 + 1 = 0 and 2 + -3 + 1 = 0

Input: arr[] = {1, -2, 1, 0, 5}

Output: 1 -2 1

Explanation: The triplets with zero-sum is 1 + -2 + 1 = 0

The Naïve Approach:

The naive approach's main principle is thoroughly examining every possible pairing of the array's three items. Every triplet is examined by the algorithm, which determines whether or not their sum equals zero. The program prints a triplet if it finds one with a zero-sum; if not, it keeps searching. Let's examine this concept's step-by-step application:

Steps to Implement the Naive Approach:

Nested Loops:

• Use three nested loops, one for each of the three possible triplet elements.
• The first loop (i), where n is the array's length, goes from 0 to n-3.
• The path of the second loop (j) is i+1 to n-2.
• Third Loop(k) traverses from j+1 to n-1.

Verify the Zero Sum:

• Please verify that the total of the components at places I, J, and K equals zero at the end of each iteration.
• Print the triplet if the sum is 0; if not, carry on with the search.

Code:

Output: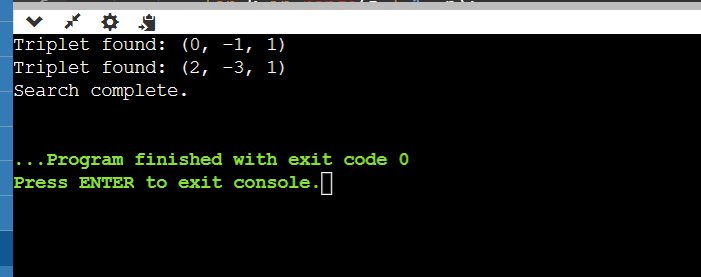

Naïve Approach Analysis:

The simplicity of the naïve approach makes it easy to find triplets whose sum is zero, but its effectiveness raises questions. This method has a cubic time complexity, or O(N^3), where N is the array's length. The three nested loops that produce a large number of iterations are the cause of this.

Time Complexity: O(n3) is the time complexity because three nested loops are needed.

Auxiliary Space: O(1), Since this is a constant space complexity no more room is needed.

Hashing Approach:

This sophisticated approach's fundamental concept is to iterate through the array and look for pairs in the remaining array that add up to -arr[i] for each entry arr[i]. This effectively turns the issue into a pair sum problem, which hashing may be used to solve quickly. The following are the steps to put this notion into practice:

How to Put the Advanced(Hashing) Approach into Practice:

Build a HashSet:

Create a HashSet from scratch to hold any unique elements that are found while traversing.

Using a Nested Loop with Hashing:

Use two iterators to execute a nested loop: an inner loop (j) that ranges from i+1 to n-1, and an outer loop (i) that ranges from 0 to n-2, where n is the length of the array.

Verify the Pair Sum in the HashSet:

• Verify whether the sum of the elements at positions i and j, multiplied by -1, is included in the HashSet for each pair of elements.
• We can print the triplet if the element is present, which means we have located one.
• Place the element at position j into the HashSet if it is absent.

Hashing Approach Implementation

Here is the Implementation of the hashing approach

Output: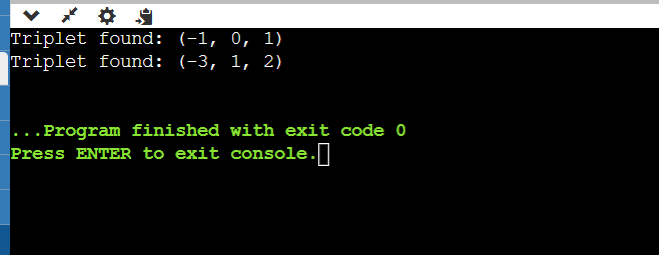

Analysis of the hashing approach

When comparing the naive approach to the hashing approach, there is an apparent reduction in the Time complexity. We can attain an O(N^2) time complexity by using hashing, where N is the array's length. This is a noticeable improvement, particularly with bigger datasets.

Time Complexity: O(n2), because two nested loops must be used, this is the needed time complexity.

Space Auxiliary: O(n), The space complexity is linear since a hash set is necessary.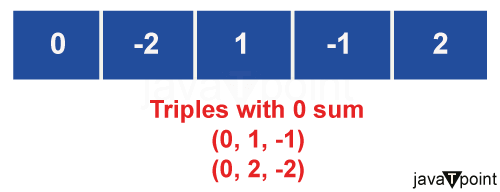

Optimal Solution:

We begin with a modified technique that further optimizes the process of identifying triplets with a zero-sum, building upon the hashing-based advanced approach. This improved method combines sorting with pointers, taking advantage of the array's sorted structure to expedite the search process. Let's examine this sophisticated but elegant solution's step-by-step execution.

The Improved Approach

We start with a refined technique that further optimizes the process of identifying triplets with a zero-sum, building upon the hashing-based advanced approach. This improved method combines sorting with pointers, taking advantage of the array's sorted structure to expedite the search process. Let's examine this complex but elegant solution's step-by-step execution.

Steps to Implement the Optimal Approach

Sort the Array:

The array should be sorted ascending. This is an important step since it allows us to use the array's sorted nature in later operations.

Traverse the Array:

• Go from beginning to end through the sorted array, treating every entry as a possible triplet's beginning.

Use Two Guidance Points:

• Make two pointers for each index i: l = i + 1 for the left pointer and r = n - 1 for the right pointer, where n is the array's length.

Search for Triplets:

• Continue until l is smaller than r.
• Verify that the total of the components at places I, L, and R equals 0.
• Print the triplet and end the loop if the sum is zero.
• Increase the value of l if the sum is less than zero.
• Reduce the value of r if the sum is larger than zero.

Optimal Approach Implementation

Let's implement the Optimal Approach using Python

Output: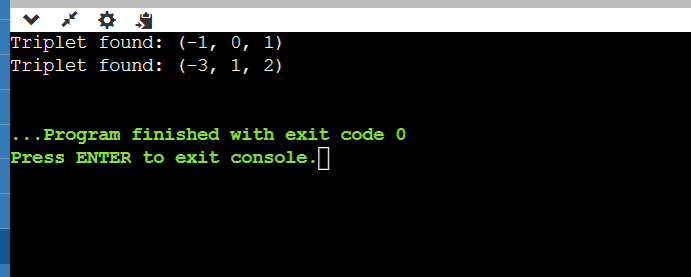

Analysis of Optimal Approach

The updated method, which combines sorting with pointers, offers a notable increase in productivity. Because to the array's sorted order and clever use of pointers, the time complexity is only O(N^2), where N is the array's length.

Time Complexity: O(n2) Since there are just two nested loops needed, O(n2) is the time complexity.

Auxiliary Space: O(1); as no additional space is needed, the space complexity remains fixed.

Conclusion:

Our examination, which aimed at understanding triplets in an array containing a zero-sum, found an algorithmic evolution pattern. We started with the basic brute-force method, which was simple but limited by cubic time complexity. Next, we moved on to the advanced hashing method, which used data structures to attain quadratic efficiency. The optimal strategy achieved the highest level by combining sorting and pointers in a smooth manner to achieve a quadratic time complexity, which reflects a tasteful blend of efficiency and elegance.

This information highlights the fundamental idea of algorithmic problem-solving, which is the careful balancing act between creativity and optimization. Computer science depends on not only solving problems but also on identifying the most elegant and efficient ways to get there. Although it may appear abstract, the search for zero-sum triplets captures the larger field of algorithmic research, where each approach demonstrates the creativity fundamental in computational thought. Finally, we show that the complexity of solutions reflects the algorithmic expertise, demonstrating the creativity and tactical thinking that are critical in the field of computational complexity.