Circular QueueWhy was the concept of the circular queue introduced?There was one limitation in the array implementation of Queue. If the rear reaches to the end position of the Queue then there might be possibility that some vacant spaces are left in the beginning which cannot be utilized. So, to overcome such limitations, the concept of the circular queue was introduced. 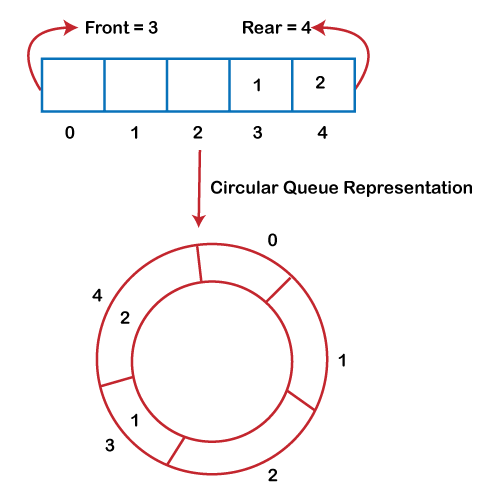
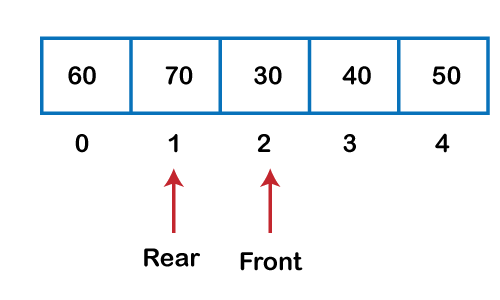
As we can see in the above image, the rear is at the last position of the Queue and front is pointing somewhere rather than the 0th position. In the above array, there are only two elements and other three positions are empty. The rear is at the last position of the Queue; if we try to insert the element then it will show that there are no empty spaces in the Queue. There is one solution to avoid such wastage of memory space by shifting both the elements at the left and adjust the front and rear end accordingly. It is not a practically good approach because shifting all the elements will consume lots of time. The efficient approach to avoid the wastage of the memory is to use the circular queue data structure. What is a Circular Queue?A circular queue is similar to a linear queue as it is also based on the FIFO (First In First Out) principle except that the last position is connected to the first position in a circular queue that forms a circle. It is also known as a Ring Buffer. Operations on Circular QueueThe following are the operations that can be performed on a circular queue:
Applications of Circular QueueThe circular Queue can be used in the following scenarios:
Enqueue operationThe steps of enqueue operation are given below:
Scenarios for inserting an elementThere are two scenarios in which queue is not full:
There are two cases in which the element cannot be inserted:
Algorithm to insert an element in a circular queue Step 1: IF (REAR+1)%MAX = FRONT Step 2: IF FRONT = -1 and REAR = -1 Step 3: SET QUEUE[REAR] = VAL Step 4: EXIT Dequeue OperationThe steps of dequeue operation are given below:
Algorithm to delete an element from the circular queue Step 1: IF FRONT = -1 Step 2: SET VAL = QUEUE[FRONT] Step 3: IF FRONT = REAR Step 4: EXIT Let's understand the enqueue and dequeue operation through the diagrammatic representation. 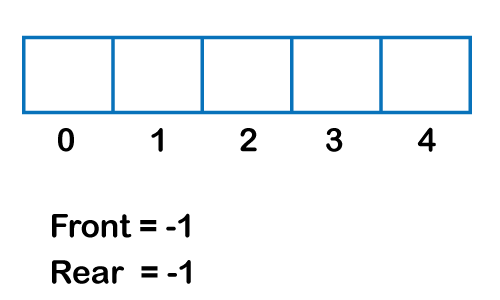
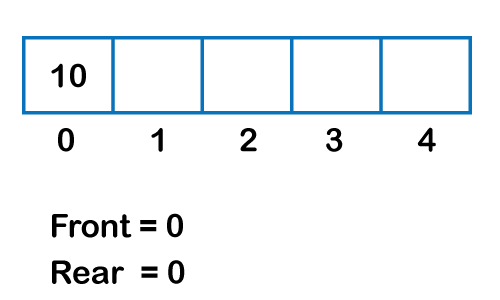
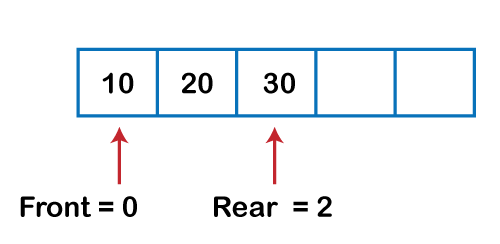
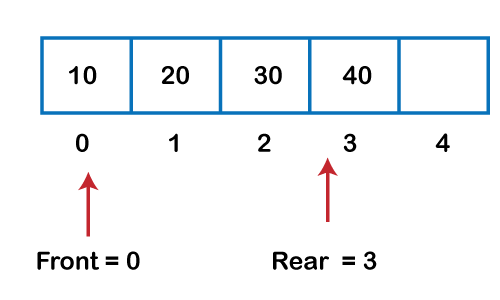
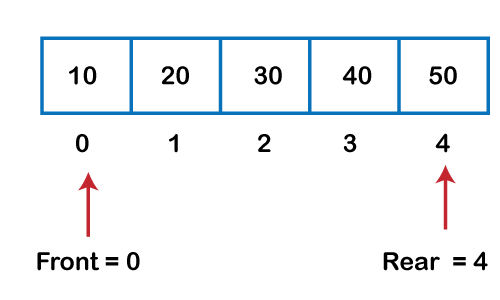
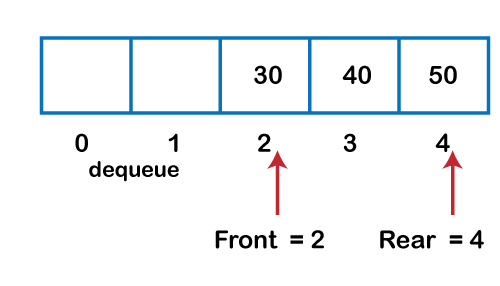
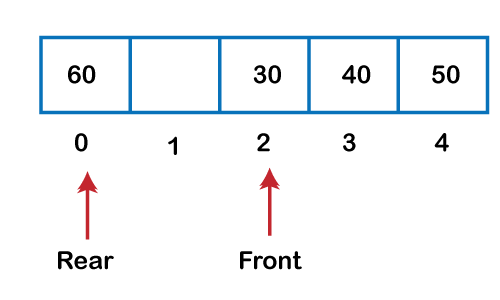
Implementation of circular queue using ArrayOutput: 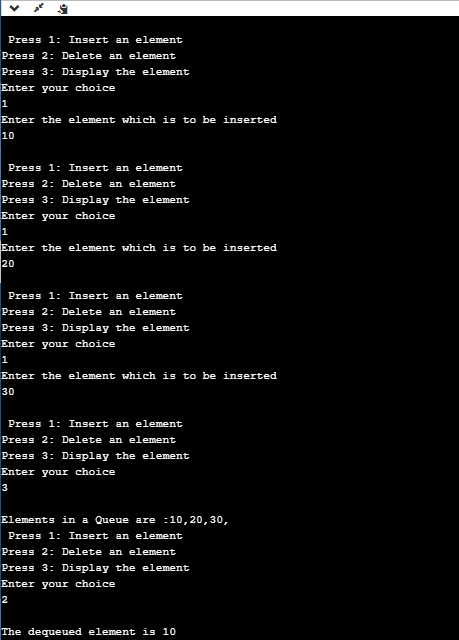
Implementation of circular queue using linked listAs we know that linked list is a linear data structure that stores two parts, i.e., data part and the address part where address part contains the address of the next node. Here, linked list is used to implement the circular queue; therefore, the linked list follows the properties of the Queue. When we are implementing the circular queue using linked list then both the enqueue and dequeue operations take O(1) time. Output: 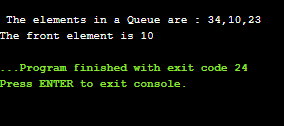
Next TopicDS Deque
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share









