What are connected graphs in data structure?
A graph is a non-linear data structure with a finite number of vertices and edges, and these edges are used to connect the vertices. Multiple runs are required to traverse through all the elements completely. Traversing in a single run is impossible to traverse the whole data structure. Each element can have multiple paths to reach another element.
- The data structure where data items are not organized sequentially is called a non-linear data structure. In other words, data elements of the non-linear data structure could be connected to more than one element to reflect a special relationship among them.
- The graph itself is categorized based on some properties; if we talk about a complete graph, it consists of the vertex set, and each vertex is connected to the other vertexes having an edge between them.
- The vertices store the data elements, while the edges represent the relationship between the vertices.
- A graph plays a very important role in various fields; the network system is represented using the graph theory and its principles in computer networks.
- Even in Maps, we consider every location a vertex, and the path derived between two locations is considered edges.
- The graph representation's main motive is to find the minimum distance between two vertexes via a minimum edge weight.
Properties of connected graphs
- We require at least two vertices and one edge to say that the graph is connected.
- It is used to store the data elements combined whenever they are not present in the contiguous memory locations.
- It is an efficient way of organizing and properly holding the data.
- It reduces the wastage of memory space by providing sufficient memory to every data element.
- Unlike in an array, we have to define the size of the array, and subsequent memory space is allocated to that array; if we don't want to store the elements till the range of the array, then the remaining memory gets wasted.
- So to overcome this factor, we will use the non-linear data structure and have multiple options to traverse from one node to another.
- Data is stored randomly in memory.
- It is comparatively difficult to implement.
- Multiple levels are involved.
- Memory utilization is effective.
About the connected graphs:
- One node is connected with another node with an edge in a graph. The graph is a non-linear data structure consisting of nodes and edges and is represented by G ( V, E ), where V stands for the set of vertices and E stands for the set of edges. The graphs are divided into various categories: directed, undirected, weighted and unweighted, etc.
- This data is not arranged in sequential contiguous locations as observed in the array. The homogeneous data elements are placed at the contiguous memory location to retrieve data elements is simpler.
- It does not have any concept of root node or child node, unlike trees. Also, it does not have any particular order of arranging the data elements like in trees, and we have a particular hierarchical order in which the data elements are arranged.
- Every tree is called a graph, and in other words, we call it a spanning tree, which has the n-1 edges, where n stands for the total number of vertices in a graph.
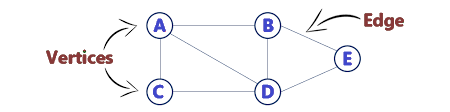
Terminologies used in the graph:
- Vertex: The data element is represented using the vertex of the graph. There is one individual vertex for a particular data element to hold a data element.
- Edge: Edges are the connecting link between two vertex nodes; it is the traversing path from one vertex node to another.
- Undirected Edge: An undirected edge is an edge between the two vertexes having no direction; it is directed for both the vertexes, which means it is a bidirectional edge.
- Directed edge: Directed edge is the edge between the two vertexes having a particular direction from one node to another node.
- Weighted edge: The edge which consists of a particular value over it, which we call a weight of the particular edge for traversing it from one vertex to the other. The weighted edges are important in finding the minimum path from one node to another.
- Degree: The degree of the vertex is defined as the total number of edges connected to that vertex.
- Indegree: The indegree of a vertex is defined as the total number of edges coming to the particular vertex.
- Outdegree: The outdegree of a vertex is defined as the total number of edges outgoing from that vertex.
Types of Connected Graph:
- Directed Graph
- Undirected graph
- Weighted graph
- Simple graph
- Multigraph
- Complete graph
Let us discuss some of its types are:
- Directed Graph: The graph consists of a directed set of edges in which every edge is associated with a particular direction. These directing edges direct the direction of the path from one vertex to another.
- Undirected graph: The graph consists of an undirected set of edges, in which every edge is connected with the vertexes but does not specify a particular direction.
- Weighted graph: The weighted graph is the graph that consists of the edges having some weights over them; it means edges consist of some value for going from one vertex to the other.
- Simple graph: Simple graph is defined as a graph that consists of only one edge between the two vertexes. Simple graphs do not consist of any parallel edges and self-loops.
- Multigraph: Multigraph consists of parallel edges and self-loops. It is more complex as compared to simple graphs.
- Complete graph: Complete graph is how each vertex is connected with every other vertex. In a complete graph, each vertex's degree must be n - 1, where n is denoted as the number of vertices.
Representation of the graph
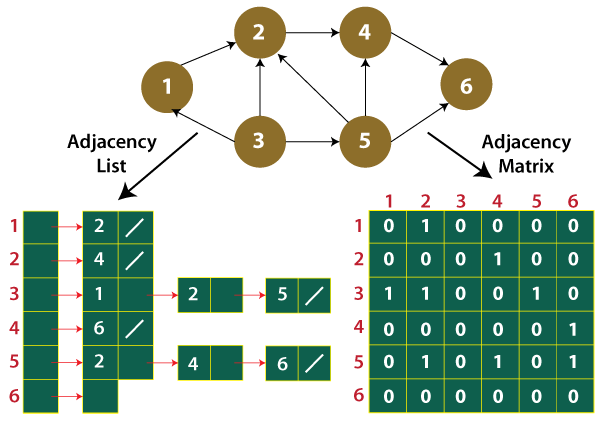
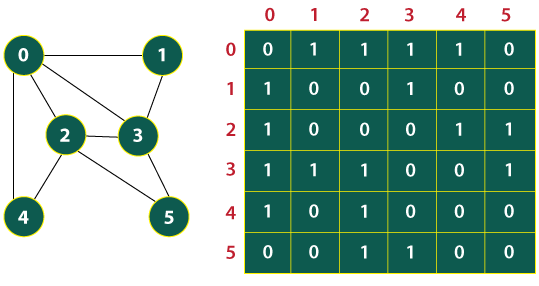
Method 1: Using Adjacency Matrix
An adjacency matrix is always a square matrix of dimension V x V, here V stands for vertices of the graph. Let G[i][j], where i denotes for row and j denotes for column. We do not have a self-loop and parallel edges in the simple connected graph. We always define G[i][i] = 0, as it denotes no connectivity, also for certain vertices, we do not have any connectivity. The adjacency matrix for an undirected graph is always symmetric. Adjacency Matrix is also used to represent weighted graphs. If adj[i][j] = w, then there is an edge from vertex i to vertex j with weight w.
- It is a sequential representation of the connectivity between the vertices.
- If we find the vertex of G [ i, j ] has an edge, then we represent it with 1.
- Otherwise, we will put 0 in the place of matrix G [ i, j ].
- If we have a weighted graph, we will simply write the edge weight at the corresponding position G [ i, j ] instead of 1.
- But if we do not have any edge, we will write 0.
- In the adjacency matrix, if we notice, we have symmetricity along the diagonal of the matrix. The portion above the diagonal in the matrix is the same as the portion below the diagonal.
- We can easily reconstruct the graph using the adjacency matrix by observing the above portion of the matrix or below.
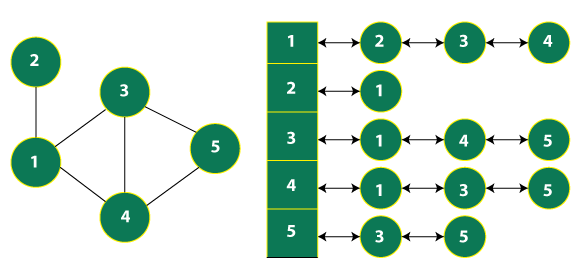
Method 2: Using Adjacency List
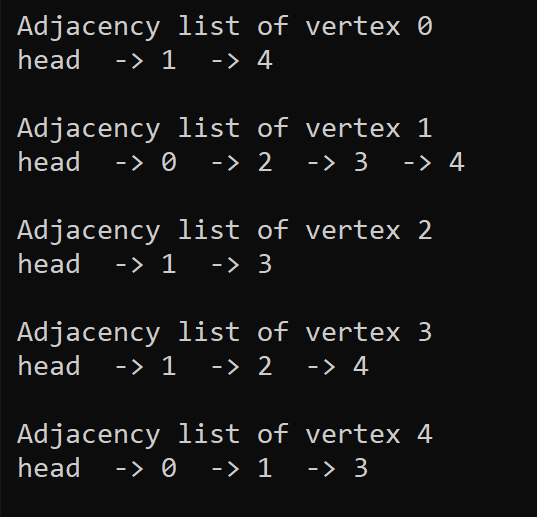
Here, an array of lists is used. The size of the array is equal to the number of vertices. Let the array be an array[]. An entry array[i] represents the list of vertices adjacent to the ith vertex. This representation can also be used to represent a weighted graph. The weights of edges can be represented as lists of pairs. Following is the adjacency list representation of the above graph.
- An adjacency list is a linked representation of the list of nodes.
- The nodes are represented in the form of the singly linked list node, and the node connectivity is shown with the help of a singly linked list.
- Suppose we have a graph in which node 1 is connected to node 2, node 3, and node 5, then in the form of the singly linked list, the head node is represented as node 1 and other nodes are present behind it, by containing the address of the next nodes.
- Similarly, in this way, the singly linked list of every node is present, which ultimately shows the connectivity of a node to the other nodes.
- The adjacency lists are more complex to represent the graph than the adjacency matrix, but adjacency matrices are simpler.
Graph traversal algorithm:
For traversing the graph, we will use some graph traversal algorithms. By using these graph traversal algorithms, we can traverse the graph easily. In traversing the graph, our main aim is to visit each graph's vertex without repeating. The sequence of the vertexes arrives while traversing is depends on the procedure of traversal we follow.
For traversing the graph, we have two methods of traversal:
- Breadth-first search
- Depth-first search
Let us discuss the above two methods in detail -
1. Breadth-first traversal:
We have to traverse the graph in breadth-first traversal by traversing each vertex. We use a queue data structure to traverse the vertex of the graph. It always starts from the root vertex or source vertex then reaches towards every connected vertex to that vertex, traversing each child node of that root node directly connected to it.
To maintain the record of each vertex's traversal, we use a queue data structure. In the queue, we will enter the vertex node that we have visited, and we will remove that vertex node from the queue, then point to the next node. Before removing the next node, we will traverse all the connected vertex nodes, and on the parallel side, makes the entries of all nodes in the queue.
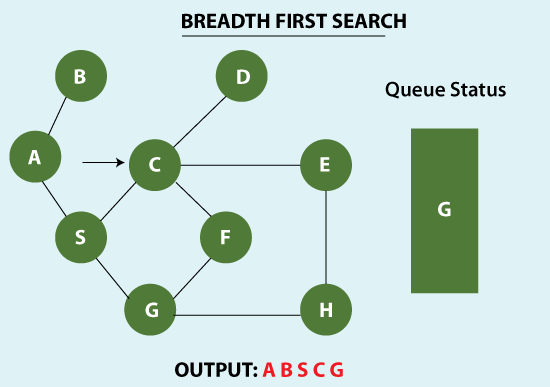
Algorithm to use Breadth-first search traversal:
- Consider a random graph, which we want to traverse.
- Choose any node as a source node, or can say root node.
- Simultaneously maintain a queue, enter that node into the queue, and write in the traversing sequence.
- Traverse all the nodes connected to the source vertex, write that sequence into the traversing sequence, and parallel do the entries into the queue.
- Remove the source node from the queue after writing all the connected nodes in the queue move towards the next node.
- As we know, the working of the queue is based on the FIFO principle. The removal of an element is done on the First in, First out criteria.
- Repeat the above steps for the next nodes until we have visited all the graph nodes.
2. Depth-first traversal:
We have to traverse the graph in depth-first traversal by traversing each vertex. We use the stack data structure to traverse the vertex of the graph. It always starts from the root vertex or can say any source vertex, then reaches towards any one of the connected vertexes. We will consider the next node as a source vertex, and then we will reach another vertex connected to the new source vertex. In this way, we traverse the whole tree and the graph data structure.
For maintaining the record of traversal of each vertex, we use stack data structure; in the stack, we will enter the vertex node that we have visited, after if we reach the end, then we will do the back traversing, visit the just previous vertex, then again repeat the same process and move in the depth of the graph, finally remove that node from the stack also, this process continues until the stack becomes empty.
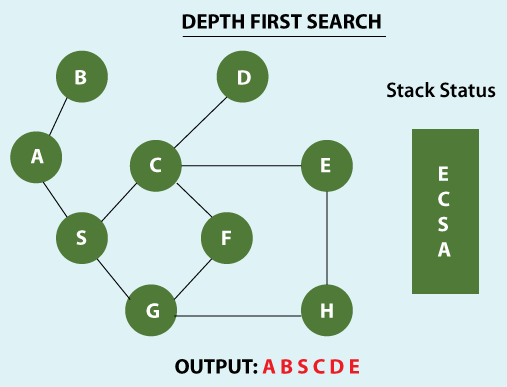
Algorithm to use Depth-first search traversal:
- Consider a random graph, which we want to traverse.
- Choose any node as a source node, or can say root node.
- Simultaneously maintain a stack, enter that node into the stack, and write in the traversing sequence.
- Traverse the next node connected to the source node and put that into the stack, then consider that node as a new source node.
- From the new source node traverse to the next level, similarly, maintain the stack and traverse the nodes until we reach the depth of the graph.
- Once we reach the depth of the graph and further cannot move to the next vertex, we do the back traversing; while doing back traversing first, we remove the current source vertex from the stack and point to the next vertex.
- Try to explore it to depth similarly in this way, and we will repeat the whole process until we cover all the vertexes of the graph.
- Repeat the above steps until the stack becomes empty.
Graph implementation in C programming language -
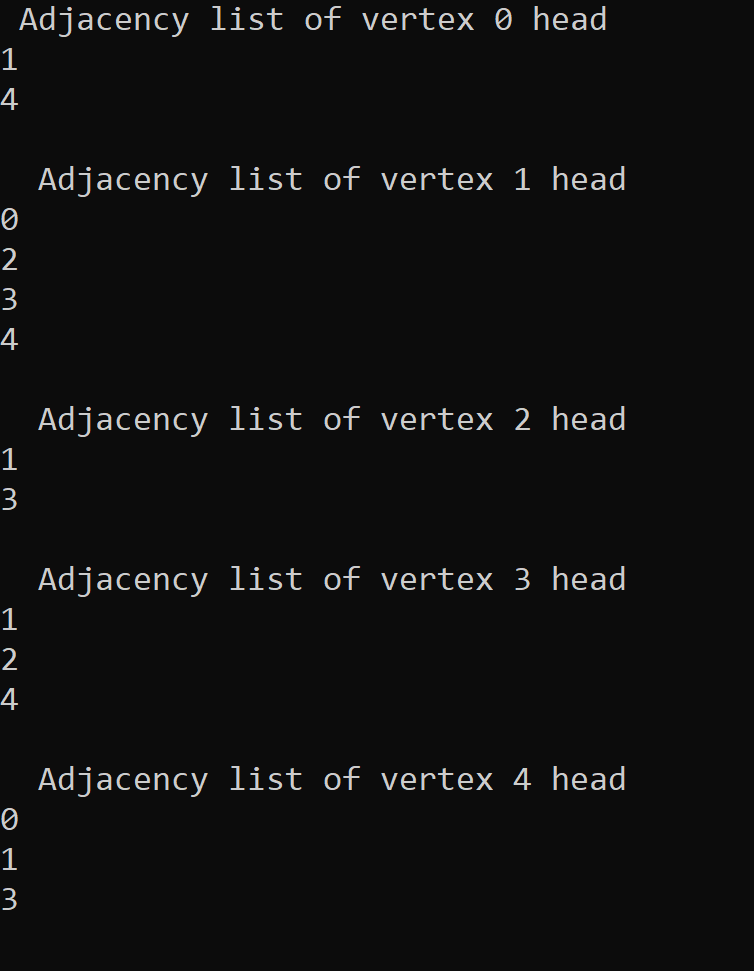
The output of the above program
Graph implementation in C++ programming language -
The output of the above program
Graph implementation in Java programming language -
The output of the above program

Graph implementation in Python programming language -
The output of the above program

Graph implementation in C# programming language -
The output of the above program

Graph implementation in Javascript programming language -
The output of the above program

|












 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now









