LEFTIST TREE / LEFTIST HEAPIntroductionA priority queue is a leftist heap or leftist tree. It is built using a binary heap variation. For each node, we store the distance to the closest leaf in the subtree anchored at that node. Let us call this value s-value. Compared to a binary heap, which is always a complete binary tree, a leftist heap strives to be extremely imbalanced. A heap is a tree-based data structure in which the element with the greatest or lowest priority is always kept at the 'root' of the tree. A heap is a complete binary tree in which all levels except the last must be entirely filled. It is also left-justified, which implies that the left subtree has been filled before the right subtree. 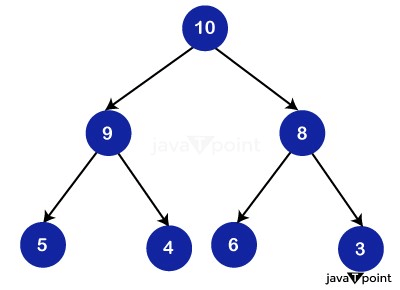
In order to ensure logarithmic performance, the entire binary tree is constantly balanced. The most widespread misperception regarding heaps is that they are sorted. However, they are only 'partially arranged' and not sorted. Furthermore, the child nodes at each level are unrelated to one another. The length of the longest subsequence in which the prefix sum at each element stays greater than zeroIntroduction The goal of this issue is to discover the longest subsequence in which the prefix sum at each element remains greater than zero. The method employs MinHeap, a widely used and useful data structure. This blog will assist you in solidifying your understanding of the Min Heap data structure. Problem Statement Determine the length of the shortest subsequence such that the prefix sum at each element remains greater than zero given an array of elements. Case Studies To better grasp the situation, consider two test cases. Test case 1: The output is 4 four the given array 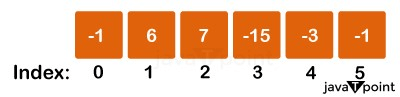

Test case 2: 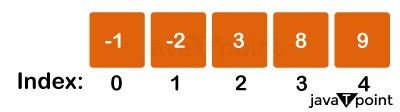
The output is 3 for the given array 
NOTE: In this problem, we must determine the length of the longest subsequence and the longest subarray. A subsequence is a non-contiguous sequence of a given sequence generated by eliminating one or more components from the original sequence.ApproachThe Min Heap data structure will be used to tackle this problem. We will go through the array and place each entry in the minimum heap. We will also add an element to the sum variable, which will keep track of the current element's prefix sum. If the prefix sum turns negative, we subtract the most negative element from the heap and pop the element in question from the heap. The Algorithm's Steps
Output Length of the longest subsequence is: 4
Time Complexity O(n*logn) since we are iterating through a for loop 'n' times. The priority queue push and pop operations take O(logn) time, making the general time complexity O(n*logn). The number n refers to the total number of items in the input vector. Space Complexity O(n), because we're utilizing a priority queue of size n. The number n indicates the number of items in the vector of inputs. Dry running of test cases To further understand the problem, consider the dry run of Test Case 1. The input array is, -1, 6, 7, -15, -3, -1 At first, sum = 0, and the Min Heap is likewise empty. -1 is added to the Min Heap, and sum = -1. 
However, as the sum goes negative, we remove the top element through the heap. The next piece, 6, is added to a heap, so the resulting sum is 6. 
The vector's next member, 7, is then examined. The current sum is 13 (6+7). As a result, 7 is likewise inserted into the heap. 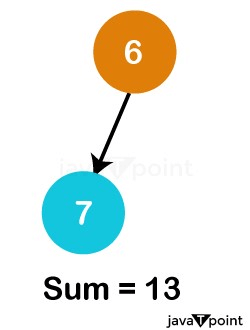
The next ingredient is -15, and adding that renders the total negative. 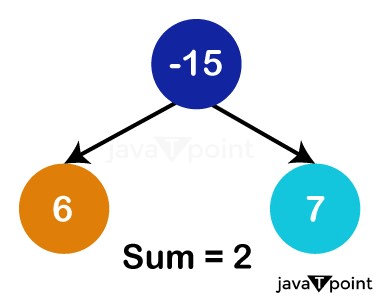
The total of the elements becomes -2, so we pop the top component of the heap once more, -15. We additionally subtract -15 from our total, making the total 13. The next member in the vector is -3; adding it to the final sum gives us 10, which is a positive number. As a result, it is added to the heap as well. 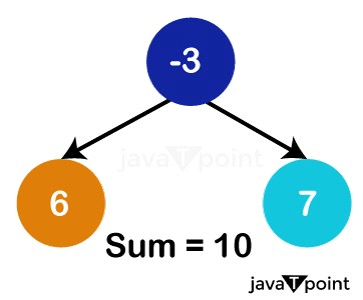
We ultimately arrive at the last element in the vector, -1, and add it to the present sum. It is also thrown into the heap. So the present sum is 9, and our Min Heap will appear like this: 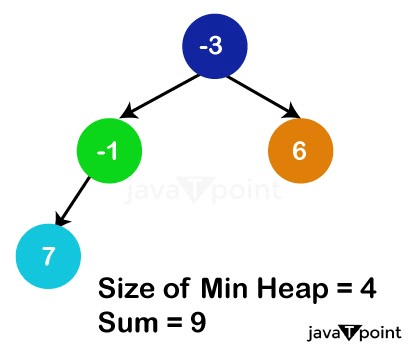
Finally, the size of our Min Heap is 4, which represents the length of the largest subsequence. Heap TypesThere are primarily two sorts of heaps: Min HeapIn a min heap, the root node represents the smallest of all the nodes in the tree because the value of every parent node is always less than or equal to the number of child nodes. 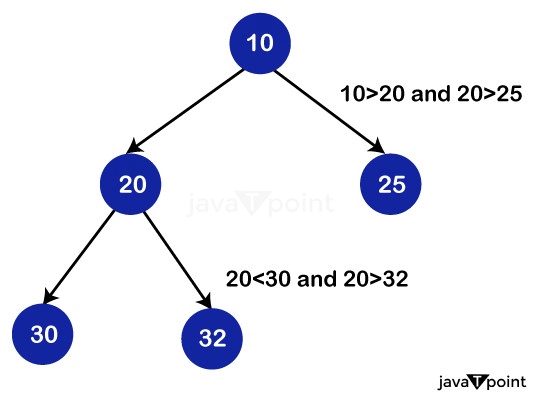
Max HeapIn a max heap, the value of all the root nodes is the greatest of all the nodes in the tree, and the value of every parent node is always larger than or equal to the value of the child nodes. 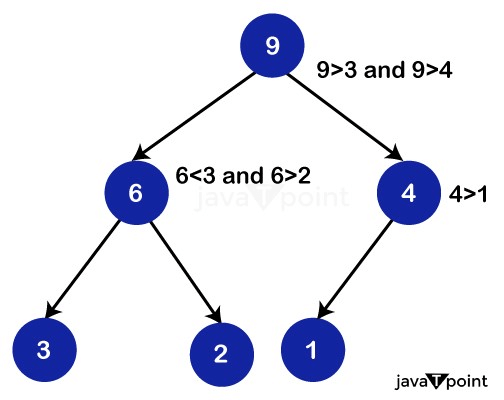
The representation of binary heaps A binary heap takes up little space and is simple to express in an array. When modelling a binary heap in an algorithm, we should keep the following points in mind: In the array: 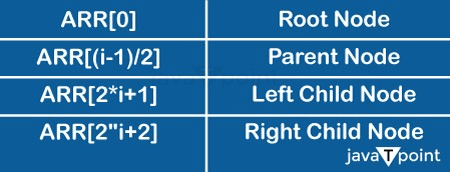
Consider the following example: 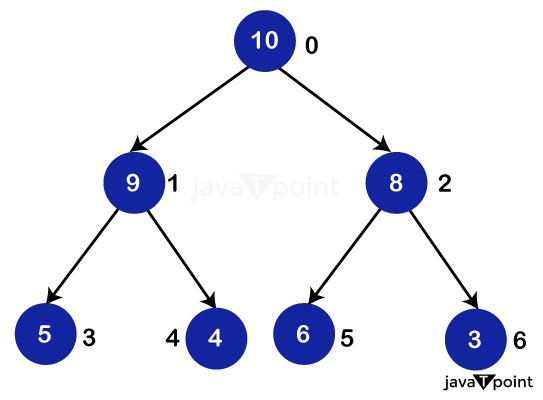
Because the binary tree shown above is complete, we can express it in an array as follows: 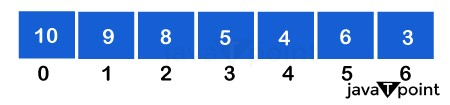
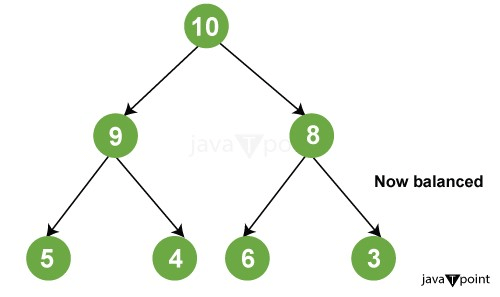
Thus, we begin with level 0, i.e., element "10," and fill it up with the first element of the array before incrementing the pointer. We are now at level 1, and we are going to fill the array with the first child node at this level, i.e., the number "9," before moving on to the number "8." Similarly, we will begin with the first member of level 2 and fill our array appropriately. A binary heap follows level sequence traversal, which means that each node on a level is visited before proceeding to the next level. In this method, a binary heap can be easily stored in an array. Binomial Heap ImplementationOperations A binary heap can be used for a variety of operations, some of which are described below: (Please keep in mind that the operations outlined below are in Max Heap terminology.) 1. maxHeapify() MaxHeapify is the programme that's in charge of restoring Max Heap's property. It arranges the node i and its subtrees in such a way that the heap property is preserved. The function is explained in depth in the following steps:
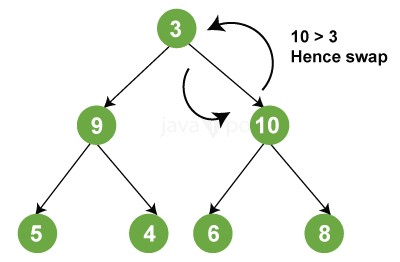
2. insertKey(): During insertion, the new element is attached to the end of the heap and becomes the array's final element. If the recently added element is smaller than the parent, nothing needs to be done. Otherwise, values are swapped until the heap attribute is restored. 3. increaseKey(): It increases the significance of a key at a specific index to some value. If this new value is less than the parent node, anything needs to be done. Otherwise, the heap property is violated, and swaps are performed to restore it. 4. getMax(): Returns the maximum element held at the bottom node of the Max heap. 6. deletekey(): The element to be eliminated is first substituted with positive infinity by using increaseKey(), and then we call removeMax() to remove it from the heap. The code below depicts the above operations. Input: Output: The current size of the heap is 7. The current maximum element is 14. The current size of the heap is 6. The current size of the heap is 8. The current maximum element is 15. Time Complexity: The following section discusses the various time complexities of binary heap functions: Construction Waste: Building a heap usually takes O(N) time. The convergence of series can be used to demonstrate it. Insertion: Inserting a new key into the heap necessitates the heapify() operation, requiring O(log (N)) time to restore the tree's order because the height of the tree is O(log (N)). As a result, the time complexity of inserting an additional key is O(log (N)). Deletion: After deleting the root node or key value, the hierarchy is heapified to restore the tree's property. As a result, the complexity is similarly given by O (log N). Obtaining the Minimum or Maximum Element: The root node stores the minimum or maximum element. As a result, it may be retrieved in a single operation, and its time complexity is O(1). Extracting the Minimum/Maximum element: Because this operation requires calling heapify() after extracting the root element in order to restore the heap's property, the time complexity is O(log(N)). 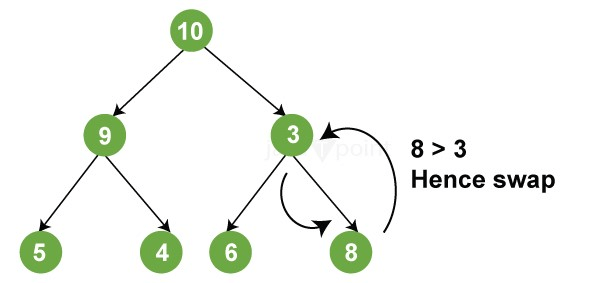
ApplicationsSome of the most important binary heap applications are:
Other Applications of Binary Heaps
Time Complexities: Following are the temporal complexities of several operations on a lefty heap:
PropertiesA lefty heap has the following properties:
We can deduce the following from the preceding properties:
Operationsmerge(): The merge operation is the primary operation of a leftist heap. deleteMin() can be used to replace the minimal node with a merge of the left and right subtrees. insert(): This is accomplished by executing the merge method on both the initial heap and a new one-node heap. S-value or DistThe s-value (or dist) of a node represents the distance that exists between the node in question and the nearest leaf in that node's subtree. A null child's dist is 0 (in certain implementations, the dist for a null child is assumed to be -1). Merging Because the right subtree of a leftist heap is smaller than the left subtree, we merge it with the other tree. |
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share









