DS Tutorial
DS Array
DS Linked List
DS Stack
DS Queue
DS Tree
DS Graph
DS Searching
DS Sorting
Differences
Misc
DS MCQ
Priority Queue using Linked listA priority queue is a type of queue in which each element in a queue is associated with some priority, and they are served based on their priorities. If the elements have the same priority, they are served based on their order in a queue. Mainly, the value of the element can be considered for assigning the priority. For example, the highest value element can be used as the highest priority element. We can also assume the lowest value element to be the highest priority element. In other cases, we can also set the priority based on our needs. The following are the functions used to implement priority queue using linked list:
The linked list of priority queue is created in such a way that the highest priority element is always added at the head of the queue. The elements are arranged in a descending order based on their priority so that it takes O(1) time in deletion. In case of insertion, we need to traverse the whole list in order to find out the suitable position based on their priority; so, this process takes O(N) time. Let's understand through an example. Consider the below-linked list that consists of elements 2, 7, 13, 15. 
Suppose we want to add the node that contains the value 1. Since the value 1 has more priority than the other nodes so we will insert the node at the beginning of the list shown as below: 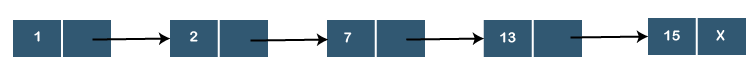
Now we have to add 7 element to the linked list. We will traverse the list to insert element 7. First, we will compare element 7 with 1; since 7 has lower priority than 1, so it will not be inserted before 7. Element 7 will be compared with the next node, i.e., 2; since element 7 has a lower priority than 2, it will not be inserted before 2.. Now, the element 7 is compared with a next element, i.e., since both the elements have the same priority so they will be served based on the first come first serve. The new element 7 will be added after the element 7 shown as below: 
Implementation in C Output 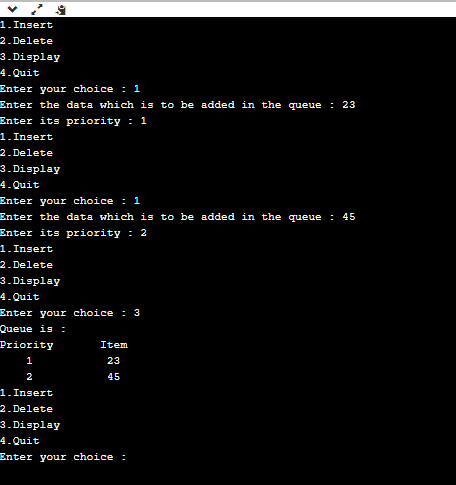
Next TopicBalanced Binary Search Tree
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share









