If you are given two traversal sequences, can you construct the binary tree?

Binary trees are fundamental data structures used to organize data hierarchically. They have many applications in computer science, from storing sorted data in binary search trees to representing expression parse trees.

A key aspect of binary trees is how to traverse them - visiting each node systematically to process or print the data it contains. The three most common traversal methods are inorder, preorder, and postorder, each producing a different node visiting order.

Given the node values in a binary tree, we can traverse it using these techniques and obtain the sequence of visited nodes. An interesting question is, if we are only given the traversal sequences, can we reconstruct the original binary tree uniquely?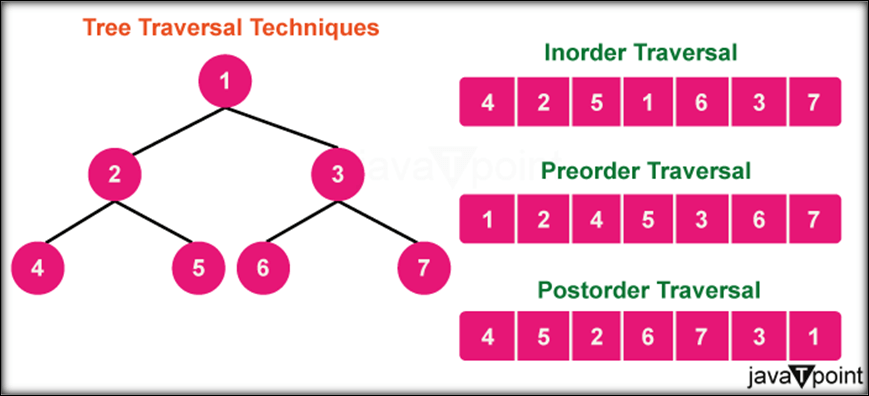

This article explores algorithms to reconstruct binary trees from their inorder and preorder (or postorder) traversal sequences. We discuss how the different traversal sequences encode information about the tree structure and node relationships. An efficient O(n^2) algorithm is presented that recursively divides the traversals to build the left and right subtrees and, hence, the original tree.

Being able to reconstruct binary trees from traversals has usefulness in several contexts. It helps recover tree structures from traversal data. It also provides insights into the properties of different traversal techniques. This algorithmic problem demonstrates how complex tree structures can be systematically processed and analyzed.

Inorder Traversal:

The inorder traversal involves traversing the left subtree first, visiting the root node, and then traversing the right subtree. For example, for the binary tree:

• Starts at the leftmost node and goes all the way to the left recursively until it reaches a leaf
• Visits the leaf node (prints it out)
• Goes to the parent node of the leaf, prints it, and then goes to the right child
• Continues this process recursively - going left, visiting, going right
• Prints out the nodes in ascending sorted order

For example, for the binary tree:

Inorder traversal prints: 4 2 5 1 3

In inorder, the root node is visited between the subtrees, so the traversal tends to produce sorted output.

Uses: Produces sorted output, so it is helpful for binary search trees.

Preorder Traversal:

The preorder traversal visits the root node first, then traverses the left subtree, followed by the right subtree. For the example tree, the preorder order would be: A, B, D, E, C

In preorder, the root node is visited first before its subtrees.

• Starts at the root node, prints it
• Goes to the left subtree recursively, prints left child nodes
• After finishing with the left subtree, visit the right subtree recursively
• Prints parent nodes before their children

For the same example tree, preorder traversal prints: 1 2 4 5 3

Uses: Creates a copy of the tree, helps in constructing the tree from traversal order

Postorder Traversal:

The postorder traversal involves traversing the left subtree first, then the right subtree, and finally visiting the root node. For the same example tree, the postorder traversal order would be: D E B C A

In postorder, the root node is visited last after the traversed subtrees.

• Starts at a leftmost node, goes all the way left and prints the leaf
• Goes to the right sibling of the leaf, prints down recursively
• After both subtrees are done, print the parent
• Prints parent nodes after their children

For the example, postorder is: 4 5 2 3 1

Uses: Deletes tree nodes safely, computes expressions with parentheses

Level Order Traversal:

The level order traversal visits tree nodes level-by-level from left to right. For the example tree, the level order traversal would be A B C D E.

The nodes are visited in increasing order of their depth or level in the tree. Level order traversal uses a queue to traverse the tree.

• Prints nodes level by level left to right
• Uses a queue to keep track of nodes
• Dequeues a node from the queue, prints it, then enqueues its children
• Continues until the queue is empty

For the example, level order traversal prints: 1 2 3 4 5

Uses: Prints level-wise hierarchy, used in breadth-first search

Algorithm to form a Binary Trees

The three standard traversal methods for a binary tree are inorder, preorder and postorder traversals. Inorder traversal visits the left subtree, the root node, and the right subtree. Preorder traversal visits the root node first, followed by the left and right subtree. Postorder traversal visits the left subtree, the right subtree, and the root node.

Out of these three traversal sequences, any two can be used to uniquely construct the original binary tree. This is because inorder traversal gives the node values in sorted order, while preorder and postorder encode the position of the root node relative to its subtrees.

The algorithm for reconstructing a binary tree given its inorder and preorder traversals is as follows:

1. Take the first element of preorder traversal. This is the root node of the tree.
2. Search for the position of this node value in the inorder traversal sequence.
3. The elements appearing before this node in order belong to the left subtree, and elements appearing after it belong to the right subtree.
4. Recursively construct the left subtree by taking the subsequence before the root node inorder and the corresponding subsequence in preorder.
5. Recursively construct the right subtree by taking the subsequences after the root node in inorder and preorder.
6. Return the root node with left and right subtrees attached appropriately.

For example, consider a binary tree with inorder traversal as DBEAFC and preorder as ABCDEF.

The first element of preorder is A - this is the root node. In inorder, DBE belong to left subtree of A, and CEF belong to right subtree. We recursively construct the left subtree using subsequence DBE in inorder and ABC in preorder. This gives us the left subtree. The right subtree is made using EF in inorder and DEF in preorder. We get the original binary tree by attaching left and right subtrees to A.

The time complexity of this algorithm is O(n^2) since finding the root node partition in inorder takes O(n) time and we repeat this for O(n) nodes. The space complexity is O(n) for the recursion stack. A similar reconstruction process applies to inorder and postorder sequences.

Here are the steps to reconstruct a binary tree given its inorder and postorder traversal sequences:

1. Take the last element of the postorder sequence. This is the root node of the tree.
2. Search for the position of this node value in the inorder sequence.
3. The elements appearing before this node in inorder belong to the left subtree, and elements after it belong to the right subtree.
4. Recursively construct the right subtree by taking the subsequence after the root node in inorder, and the corresponding subsequence in postorder (excluding the last element which is the root).
5. Recursively construct the left subtree by taking the subsequences before the root node in inorder and postorder.
6. Return the root node with the right and left subtrees attached appropriately.

The key differences between using inorder and preorder are:

• We take the last element of postorder instead of the first element of preorder to get the root node.
• We recursively construct the right subtree before the left subtree since postorder visits right subtree before left.

For example, if the inorder sequence is DBEAFC and the postorder is DEBFCA, then:

• The last element of the postorder is A, which is the root node.
• In inorder, DBE are left subtree and CEF are right subtree of A.
• Construct the right subtree with EF in inorder and EBF in postorder by recursively calling the algorithm.
• Construct the left subtree with DBE in inorder and postorder.
• Return root node A with left and right subtrees attached.

This reconstructs the original binary tree from inorder and postorder traversals. The overall time and space complexity is the same as using inorder and preorder.

In summary, given any two inorder, preorder and postorder traversals, we can uniquely reconstruct the original binary tree. The key lies in using one sequence (in order) to identify node relationships and the root node position from the other sequence to recursively build subtrees systematically. This demonstrates how different traversal methods encode complementary information about a binary tree structure.