Types of Hash Functions in C

Hashing is the technique/ process of mapping key: value pairs by calculating a Hash code using the Hash Function. When given a (key: value) pair, the Hash Function calculates a small integer value from the key. The obtained integer is called the Hash value/ Hash code and acts as the index to store the corresponding value inside the Hash Table.

If for two (key: value) pairs, the same index is obtained after applying the Hash Function, this condition is called Collision. We need to choose a Hash Function such that Collision doesn't occur.

Terminology:

1. Hashing: The whole process
2. Hash value/ code: The index in the Hash Table for storing the value obtained after computing the Hash Function on the corresponding key.
3. Hash Table: The data structure associated with hashing in which keys are mapped with values stored in the array.
4. Hash Function/ Hash: The mathematical function to be applied on keys to obtain indexes for their corresponding values into the Hash Table.

This article explains different types of Hash Functions programmers frequently use. These are the four Hash Functions we can choose based on the key being numeric or alphanumeric:

1. Division Method
2. Mid Square Method
3. Folding Method
4. Multiplication Method

1. Division Method:

Say that we have a Hash Table of size 'S', and we want to store a (key, value) pair in the Hash Table. The Hash Function, according to the Division method, would be:

• Here M is an integer value used for calculating the Hash value, and M should be greater than S. Sometimes, S is used as M.
• This is the simplest and easiest method to obtain a Hash value.
• The best practice is using this method when M is a prime number, as we can distribute all the keys uniformly.
• It is also fast as it requires only one computation - modulus.

Let us now take an example to understand the cons of this method:

Size of the Hash Table = 5 (M, S)

Key: Value pairs: {10: "Sudha", 11: "Venkat", 12: "Jeevani"}

For every pair:

1. {10: "Sudha"}
   Key mod M = 10 mod 5 = 0
2. {11: "Venkat"}
   Key mod M = 11 mod 5 = 1
3. {12: "Jeevani"}
   Key mod M = 12 mod 5 = 2

Observe that the Hash values were consecutive. This is the disadvantage of this type of Hash Function. We get consecutive indexes for consecutive keys, leading to poor performance due to decreased security. Sometimes, we need to analyze many consequences while choosing the Hash Table size.

A simple program to demonstrate the mechanism of the division method:

Output:

Enter the size of the Hash Table: 5
The indexes of the values in the Hash Table: 0 1 2

2. Mid Square Method:

It is a two-step process of computing the Hash value. Given a {key: value} pair, the Hash Function would be calculated by:

1. Square the key -> key * key
2. Choose some digits from the middle of the number to obtain the Hash value.

We should choose the number of digits to extract based on the size of the Hash Table. Suppose the Hash Table size is 100; indexes will range from 0 to 99. Hence, we should select 2 digits from the middle.

Suppose the size of the Hash Table is 10 and the key: value pairs are:

{10: "Sudha, 11: "Venkat", 12: "Jeevani"}

Number of digits to be selected: Indexes: (0 - 9), so 1

H(10) = 10 * 10 = 100 = 0

H(11) = 11 * 11 = 121 = 2

H(12) = 12 * 12 = 144 = 4

• All the digits in the key are utilized to contribute to the index, thus increasing the performance of the Data Structure.
• If the key is a large value, squaring it further increases the value, which is considered the con.
• Collisions might occur, too, but we can try to reduce or handle them.
• Another important point here is that, with the huge numbers, we need to take care of overflow conditions. For suppose, if we take a 6-digit key, we get a 12-digit number that exceeds the range of defined integers when we square it. We can use the long int or string multiplication technique.

A simple program to demonstrate the mechanism of the mid-square method:

3. Folding Method

Given a {key: value} pair and the table size is 100 (0 - 99 indexes), the key is broken down into 2 segments each except the last segment. The last segment can have less number of digits. Now, the Hash Function would be:

• The last carry with fewer digits can be ignored in calculating the Hash value.

For suppose "k" is a 10-digit key and the size of the table is 100(0 - 99), k is divided into:

sum = (k1k2) + (k3k4) + (k5k6) + (k7k8) + (k9k10)

Now, H(x) = sum % 100

Let us now take an example:

The {key: value} pairs: {1234: "Sudha", 5678: "Venkat"}

Size of the table: 100 (0 - 99)

For {1234: "Sudha"}:

1234 = 12 + 34 = 46

46 % 100 = 46

For {5678: "Venkat"}:

5678 = 56 + 78 = 134

134 % 99 = 35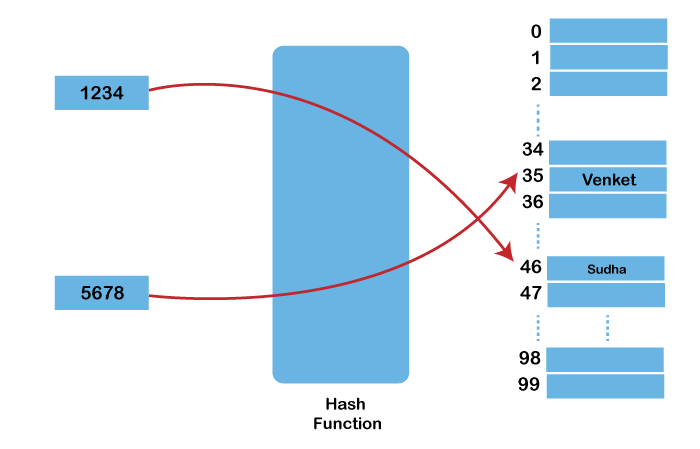

4. Multiplication method

Unlike the three methods above, this method has more steps involved:

1. We must choose a constant between 0 and 1, say, A.
2. Multiply the key with the chosen A.
3. Now, take the fractional part from the product and multiply it by the table size.
4. The Hash will be the floor (only the integer part) of the above result.

So, the Hash Function under this method will be:

For example:

{Key: value} pairs: {1234: "Sudha", 5678: "Venkat"}

Size of the table: 100

A = 0.56

For {1234: "Sudha"}:

H(1234) = floor(size(1234*0.56 mod 1))

= floor(100 * 0.04)

= floor(4) = 4

For {5678: "Venkat"}:

H(5678) = floor(size(5678*0.56 mod 1))

= floor(99 * 0.68)

= floor(67.32)

= 67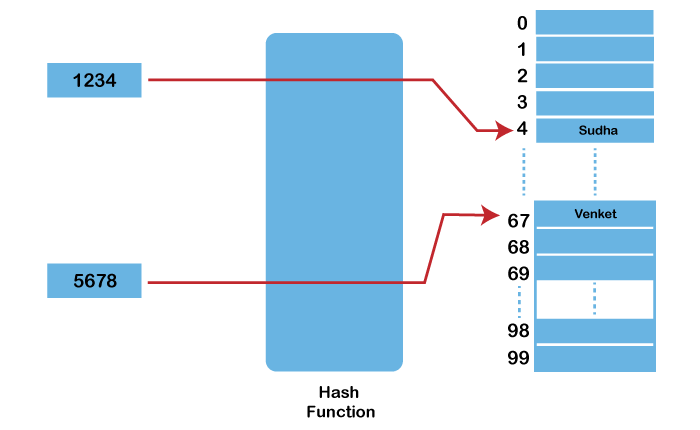

• It is considered best practice to use the multiplication method when the Hash Table size is a power of 2 as it makes the access and all the operations faster.

What after computing the Hash value?

After computing the Hash value using the hash Function, this value is used as an index in the Hash table. Whenever the user wants to access a value, the corresponding key is hashed using the Hash Function, which gives the index of the key's value in the Hash Table with less cost than regular arrays and linked lists. Hence, Hashing is used to reduce the Time as well as space complexity of the program.