Bloom Filters

A Bloom filter is a space-efficient probabilistic data structure that is used to test whether an element is a member of a set. It was conceived by Burton Howard Bloom in 1970. The primary advantage of a Bloom filter over other data structures is its impressive space and time efficiency.

Understanding Bloom Filters

Under the hood, a Bloom filter is an array of bits, all set to zero initially. The size of this bit array depends on the number of elements expected to be stored and the desired false positive rate.

A Bloom filter uses multiple hash functions to map each element to one or more array indexes. When an element is added to the filter, the bits at the hashed indexes are set to 1. When querying for an element, the filter checks the bits at the hashed indexes. If any of the bits are 0, the element is not in the set. If all bits are 1, the element might be in the set.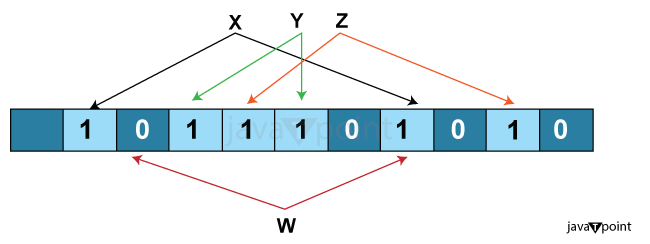

Key Properties of Bloom Filters

Space Efficiency: A Bloom filter out makes use of significantly less space than other records structures like hash tables or binary search bushes.
Time Efficiency: The time to add an element or check for club is steady, i.e., O(1), and does no longer boom as extra elements are delivered.
No False Negatives: If an element has been added to the clear out, a question will usually verify that it's far inside the set.
Possible False Positives: If a detail has no longer been delivered to the filter out, a question will commonly successfully file that it isn't in the set. However, there's a sure opportunity of a fake fine, i.e., the filter out incorrectly reporting that the element is inside the set.

Bloom Filter Operations

A Bloom filter supports two primary operations:

Insert: This operation adds an element to the filter. The element is hashed to multiple array indexes, and the bits at these indexes are set to 1.
Lookup: This operation checks whether an element is in the filter. The element is hashed to multiple array indexes, and the bits at these indexes are checked. If any bit is 0, the element is not in the set. If all bits are 1, the element might be in the set.

Bloom filter Working

Take a binary array of 'm' bits initialized with 0 for up to n different elements, set 'k' bits to at least one within the position chosen via the output of all the n exceptional factors after passing through hash functions. Now take the detail you want to perceive if it's far already present or no longer. Pass it through the equal hash characteristic, if all bits are set, the detail probable already exists, with a fake tremendous charge of p; if any of the bits are not set, the detail does no longer exist.

Example of a Bloom Filter

Consider a Bloom filter with a bit array of size 10 and three hash functions. Let's add the string "hello" to the filter. Suppose the hash functions map "hello" to the indexes 1, 3, and 7. The bit array after the insert operation would look like this:

0 1 0 1 0 0 0 1 0 0

Now, if we perform a lookup for "hello", the filter checks the bits at indexes 1, 3, and 7. Since all these bits are 1, the filter reports that "hello" might be in the set.

Understanding using code:

import math
import mmh3
from bitarray import bitarray

class BloomFilter:
    def __init__(self, items_count, fp_prob):
        self.fp_prob = fp_prob
        self.size = self._get_size(items_count, fp_prob)
        self.hash_count = self._get_hash_count(self.size, items_count)
        self.bit_array = bitarray(self.size)
        self.bit_array.setall(0)

    def add(self, item):
        for i in range(self.hash_count):
            digest = mmh3.hash(item, i) % self.size
            self.bit_array[digest] = True

    def check(self, item):
        for i in range(self.hash_count):
            digest = mmh3.hash(item, i) % self.size
            if not self.bit_array[digest]:
                return False
        return True

    @staticmethod
    def _get_size(n, p):
        m = -(n * math.log(p)) / (math.log(2) ** 2)
        return int(m)

    @staticmethod
    def _get_hash_count(m, n):
        k = (m / n) * math.log(2)
        return int(k)

if __name__ == "__main__":
    n = 30  # no of items to add
    p = 0.01  # false positive probability

    bloomf = BloomFilter(n, p)
    print(f"Bit array size: {bloomf.size}")
    print(f"False positive rate: {bloomf.fp_prob}")
    print(f"Hash functions count: {bloomf.hash_count}")

    # words to be added
    word_present = ['apple', 'banana', 'mango', 'strawberry', 'grapefruit',
                    'kiwi', 'peach', 'plum', 'nectarine', 'lime', 'lemon',
                    'orange', 'pineapple', 'raspberry', 'blueberry', 'blackberry',
                    'watermelon', 'cantaloupe', 'papaya', 'guava', 'pomegranate']

    # word not added
    word_absent = ['potato', 'tomato', 'onion', 'lettuce', 'spinach',
                   'broccoli', 'carrot', 'pepper', 'cucumber', 'celery',
                   'asparagus', 'cauliflower', 'mushroom', 'squash', 'zucchini']

    for item in word_present:
        bloomf.add(item)

    test_words = word_present[:15] + word_absent

    for word in test_words:
        if bloomf.check(word):
            if word in word_absent:
                print(f"'{word}' is a false positive!")
            else:
                print(f"'{word}' is likely present!")
        else:
            print(f"'{word}' is certainly not present!")

Output:

Applications of Bloom Filters

Bloom filters are used in various applications where space efficiency is crucial. They are used in databases, caches, routers, and other systems to quickly decide whether a given item is in a set. For example, a web browser might use a Bloom filter to check whether a URL is in a set of malicious URLs.

Limitations of Bloom Filters

While Bloom filters are highly space and time-efficient, they do come with some limitations:

False Positives: As mentioned earlier, a Bloom filter can sometimes incorrectly report that an element is in the set.
No Deletion: Removing an element from a Bloom filter is not straightforward because clearing a bit might remove other elements that share the same bit.
No Element Retrieval: A Bloom filter does not store the actual elements, so you cannot retrieve an element from a Bloom filter.

Despite these limitations, Bloom filters are a powerful tool when used in the right context. Their space and time efficiency make them an excellent choice for large-scale systems that need to test set membership quickly and efficiently.

Optimizing Bloom Filters

While Bloom filters are already space-efficient, there are ways to optimize them further:

Choosing the Right Size: The size of the bit array (m) and the number of hash functions (k) can significantly impact the performance of a Bloom filter. A larger bit array will reduce the probability of false positives but will consume more memory. Similarly, more hash functions will reduce false positives but increase the time complexity of insertions and lookups.
Multiple Hash Functions: The choice of hash functions is crucial. Good hash functions for Bloom filters should be independent (the output of one function doesn't affect the output of another) and uniformly distributed (each bit in the array has an equal chance of being set to 1).
Double Hashing: Instead of using multiple hash functions, we can use two hash functions to simulate additional ones. This technique, known as double hashing, can save computation time.

Next TopicCount Array Pairs Divisible by k

← prev next →