Fibonacci Heap

In this article, we will learn about the Fibonacci heap, its properties, advantages and, later on, its implementation: Before discussing the Fibonacci heap, let us first take a quick overview of ideas used in building a Fibonacci heap:

What are heaps in data structure?

Heaps are the abstract data type which is used to show the relationship between parents and children: Heap is categorized into Min-Heap and Max-Heap:

1. A min-heap is a tree in which, for all the nodes, the key value of the parent must be smaller than the key value of the children.
2. A max-heap is a tree in which, for all the nodes, the key value of the parent must be greater than the key value of the children.

What is a circular doubly-linked list in data structure?

A doubly-linked list is the advanced version of the singly-linked list. Each node in a double-linked list contains two pointers left and right pointers. The left-pointer points to its left node, and the right-pointer points to the right node. The right pointer of the last node points to the first node, and the left pointer of the first node points to the last node. The figure shows how a circular doubly-linked list is observed:

Let us now discuss the Fibonacci heap:

Define Fibonacci Heap:

Fibonacci Heap - A Fibonacci heap is defined as the collection of rooted-tree in which all the trees must hold the property of Min-heap. That is, for all the nodes, the key value of the parent node should be greater than the key value of the parent node:

The given figure is an example of the Fibonacci tree: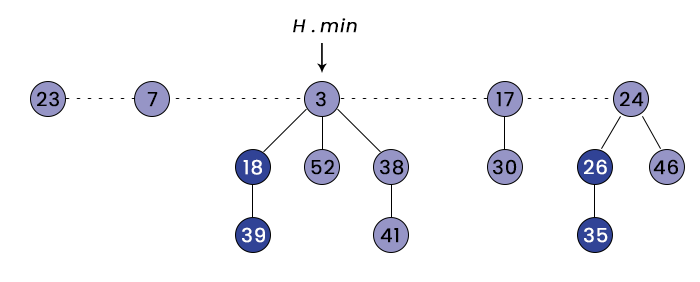

The above Fibonacci Heap consists of five rooted min-heap-ordered trees with 14 nodes. The min-heap-ordered tree means the tree which holds the property of a min-heap. The dashed line shows the root list. The minimum node in the Fibonacci heap is the node containing the key = 3 pointed by the pointer FH-min.

Here, 18, 39, 26, and 35 are marked nodes, meaning they have lost one child. The potential of the Fibonacci series = No. of rooted tree + Twice the number of marked nodes = 5 + 2 * 4 = 13.

Let us now observe the above example with the complete representation of the Fibonacci Heap: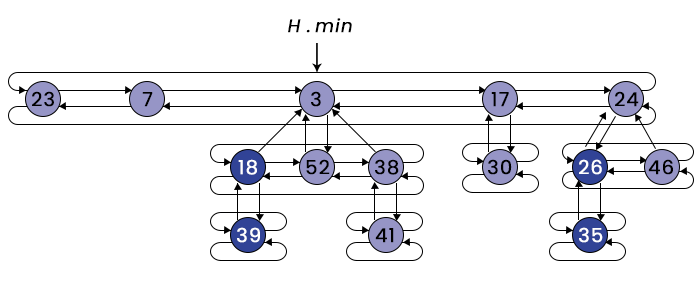

In the above figure, we can observe that each node contains four pointers, the parent points to the parent (Upward), the child points to the child (downward), and the left and right pointers for the siblings (sideways).

Properties of Fibonacci Heap:

1. It can have multiple trees of equal degrees, and each tree doesn't need to have 2^k nodes.
2. All the trees in the Fibonacci Heap are rooted but not ordered.
3. All the roots and siblings are stored in a separated circular-doubly-linked list.
4. The degree of a node is the number of its children. Node X -> degree = Number of X's children.
5. Each node has a mark-attribute in which it is marked TRUE or FALSE. The FALSE indicates the node has not any of its children. The TRUE represents that the node has lost one child. The newly created node is marked FALSE.
6. The potential function of the Fibonacci heap is F(FH) = t[FH] + 2 * m[FH]
7. The Fibonacci Heap (FH) has some important technicalities listed below:
   1. min[FH] - Pointer points to the minimum node in the Fibonacci Heap
   2. n[FH] - Determines the number of nodes
   3. t[FH] - Determines the number of rooted trees
   4. m[FH] - Determines the number of marked nodes
   5. F(FH) - Potential Function.

The time complexities of different operations performed on a Fibonacci heap are listed below in the table:

1. Creating a Fibonacci Heap:

In an empty Fibonacci Heap (FH)

The number of rooted trees, t(FH) = zero,

The minimum node, FH -> min = NIL,

Number of nodes, FH -> n = 0,

Number of marked nodes, FH -> m = 0, and

The potential of the empty Fibonacci heap ?(FH) = 0.

It is created by the MAKE-FIB-HEAP, which allocates and returns the Fibonacci heap object, FH in amortized cost O(1) equal to its actual cost: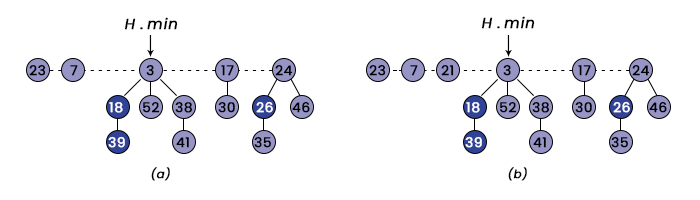

Insertion of a node:

The below pseudo code of INSERT-FIB-HEAP inserts a node x in the Fibonacci heap, FH. Assume that the node x has already been allocated and x -> key is already filled:

Line-wise explanation of the INSERT_FIB_HEAP (FH, X) pseudo-code:

1. Initializing the degree of the node x = 0
2. Initializing the parent of the node x = NIL
3. Initializing the child of the node x = NIL
4. Marking FALSE in the mark attribute of the x
5. If-condition checks whether the Fibonacci heap (FH) is empty or not
6. If yes, the creates a new root list and adds x to it
7. Making the newly added x the minimum node
8. If the if-condition fails
9. Inserts the x in the root list
10. Checks whether the x -> key is smaller than the FH -> min
11. If yes, then it makes the x the minimum node of the FH by updating the FH -> min = x
12. In the last line, it increases the number of nodes of the FH by 1

2. Union of two Fibonacci Heap:

The below pseudo-code simply concatenates the root lists of two Fibonacci heaps, FH1 and FH2 and destroys both of them during the process, determines the min node and returns the new Fibonacci heap, FH.

Line-wise explanation of UNION-FIB-HEAP (FH1, FH2) pseudo-code:

1. Creates a new Root List FH
2. Set the min -> FH = min -> FH1; the minimum node of the FH is now the minimum node of FH1.
3. Joins (Concatenates) the root list of FH2 with the root list of FH
4. Checks whether the min -> FH1 is null, min -> FH2 is null, and whether the min -> FH2 is smaller than the min -> FH1 or not
5. If yes, it sets the min -> FH = min -> FH2
6. Number of nodes in FH = sum of the number of nodes in FH1 and FH2
7. Returning the FH

3. Extracting the Minimum Node:

The extraction of minimum Node is one of the most complicated operations performed on the Fibonacci Heap. It is also where the delayed work of consolidating trees in the root list finally occurs. The below pseudo-code extracts the minimum node of the Fibonacci tree. For ease of use, the code assumes that when a node is removed from a linked list, pointers in the list are updated but not pointers in the extracted node. Additionally, it invokes the auxiliary procedure CONSOLIDATE, which we'll see in a moment.

Line-wise explanation of EXTRACT-MIN-FIB-HEAP (FH) pseudo-code:

1. Saves the min pointer in Y
2. Checks if the Fibonacci heap is empty or not
3. If not, then it Runs a loop for all the children of Y
4. Adds the children of Y in the root list
5. Set the parent attributes = NIL for all the children
6. Deletes the Y node from the root list
7. If the right pointer of the Y is equal to the Y, it means that it was the only node in the Fibonacci heap.
8. If Y was the only node setting, the FH -> min = NIL. Fibonacci heap is empty now.
9. Else part run if there is another node in the root list of FH
10. Sets the min -> FH = Y -> Right; now, min points to a different node present on the right of the node (Note: Root list is a circular doubly linked list)
11. Calls the CONSOLIDATE (FH) function, which we have discussed below:
12. Decreases the number of nodes of FH by 1
13. Returning Y

Line-wise explanation of the CONSOLIDATE (FH) pseudo-code: 2544

1. In line 1, it creates a new array of size D (FH -> N)

2. In lines 2 and 3, it fills NIL at all indexes of A.

3. - In lines 4 to 15, it executes the same process for all the nodes present in the root list. It selects each node 'W' from the root list and stores it in 'X'. Then, it stores the degree of X in d and runs a while loop if, at index d, it is not NIL. But initially, all the values are NIL, so, it won't execute, and in line 14, it stores 'X' at index d. Now, the idea of while is to check whether there is any node present in the root list of the same degree as of 'X'.

In the second iteration of the for-loop, it selects another node from the root list and stores it in X and its degree in d. The while condition becomes true if there is a node in the root list of the same degree as of 'X'. Suppose the condition of the while-loop is true. Now, it stores the node of the same degree as of 'X' in Y and checks which has the larger key. If Y has a key larger than the key of X., it swaps both of them and calls LINK-FIB-HEAP (FH, Y, X) to delete the Y from the root list after making it a child of X, and it also increases the degree of X by one after that.

In line 12, it removes the element stored at index d in the array and increases the value of d by 1.

The whole idea of the code is to have exactly one node of each degree in the root list and make other nodes a child of them without violating the condition of the Fibonacci heap.

4. In lines 16 to 24, It runs a for loop for all the nodes stored in the array. Firstly, it checks whether there is an element present in the array at index I or not. If yes, then it executes the other peace of codes. Now, it checks whether the min of FH is NIL or not. If yes, then it creates a root list and stores the A[I] into it and makes the FH -> min points to it. If not, then it inserts the A[I] into the root list and compares its key value with the min -> key. Whosoever has the smallest key, FH -> min will point to the smallest of them.

Line-wise explanation of the LINK-FIB-HEAP (FH, Y, X) pseudo-code:

1. It removes the Y from the root list

2. Makes the Y nodes a child of X and increases the degree of X by 1

3. Marks FALSE in the Y -> mark.

4. Decreasing a Key

Decreasing a key is performed on the Fibonacci heap to decrease the key of any node and can be performed in the O(1) amortized time. In the below pseudo code, we have assumed that removing a from the linked list does not change any of the structural attributes in the removed node.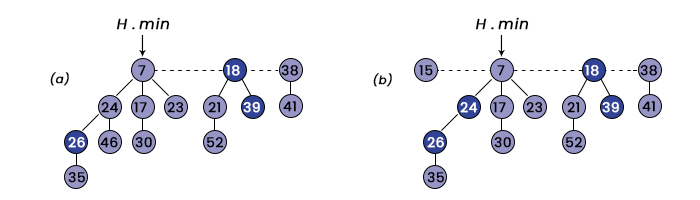

1. Is the actual Fibonacci heap and
2. represents the heap after decreasing the node storing key = 45 to 15.

Line-wise explanation of DECREASE-Key-FIB-HEAP (FH, X, K) pseudo-code:

1. In lines 1 to 2, it checks whether the key entered is greater than the existing key or not. If yes, the program terminates and will not change anything in the Fibonacci heap.

2. In line 3, Updates the key of X; now, X -> Key is equal to the k

3. In line 4, It stores the parent of X in Y

4. In line 5, The if condition will become true only if the node X does not belong to the root list, i.e., there exists a parent of it, and the key of X must be smaller than the key of Y.

5. In line 6, it calls CUT (FH, X, Y) to remove X from the F and add it to the root list

6. In line 7, It calls CASCADING-CUT (FH, Y) to mark True in Y or to remove it from the linked list and add it to the root list.

7. In line 8, It checks whether the X has the key smaller than the FIB -> min -> Key or not

8. In line 9, if the condition is satisfied then it makes X the min of the Fibonacci heap.

Explanation of CUT (FH, X, Y) Pseudo-code:

In the above pseudo-code, it first finds the parent of Y and stores it in Z. Then, it checks whether the Y is in the root list or not. If not means Z is not equal to NIL, Again, it checks whether it is marked or not, If it is marked FALSE then it changes it to TRUE and the control returns to the FIB-DECREASE-KEY. If it is marked TRUE, then it removes Y from Z and places Y in the root list and repeats the same process and stops when one of the parent nodes is found unmarked.

5. Deleting a Node:

The deleting a node from an n-node Fibonacci heap can be performed in O(D(n)) amortized cost time. In the below pseudo-code, we have assumed that as of now there is no key value of -infinity in the heap.

The DECREASE-KEY-FIB-HEAP (FH, X, -∞) decreases the key of X and makes it the smallest possible value i.e., -infinity. The EXTRACT-MIN-HEAP function removes X from the Fibonacci heap. It can be concluded that the amortized cost of the DELETE-FIB-HEAP is the sum of the amortized cost of DECREASE-KEY-FIB-HEAP (O(1)) and the amortized cost of the EXTRACT-MIN-HEAP (O(D(n)).