Segment Tree - Sum of given Range

Let us consider the following problem to understand Segment Trees.

We have an array arr[0... n-1]. We should be able to

Find the sum of elements from index l to r where 0 <= l <= r <= n-1
Change the value of a specified element of the array to a new value x. We need to do arr[i] = x where 0 <= i <= n-1.

Range sum with nested loops:

Running a loop from l to r and computing the sum of the elements in the provided range is a straightforward solution. Just enter arr[i] = x to change a value. While the first operation requires O(n) time, the second only needs O(1) time.

Range total using Prefix Sum:

An alternative is to make a new array and place the total from start to I at the ith index. The update procedure now requires O(n) time, while the total of a given range can be calculated in O(1) time. If there are many query operations and little updates, this works nicely.

Range total using a segment tree:

The most effective method is to utilise a segment tree; we can do both operations using a segment tree in O(log(N)) time.

Segment tree representation

The elements in the input array are Leaf Nodes.
Each internal node shows how the leaf nodes have merged in some way. For certain issues, there can be a different merging. Summarizing the leaf nodes under a node is merging for this issue.
Segment Trees are shown as an array representation of a tree. The left child of each node at index I is at index (2*i+1), the right child is at index (2*i+2), and the parent is at index I - 1) / 2).

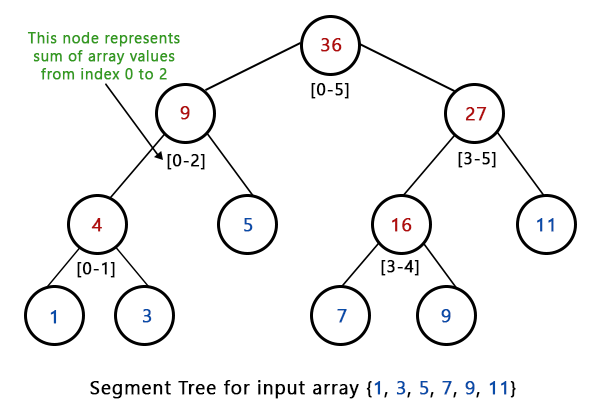
Building a segment tree from the supplied array

We begin by examining the segment arr[0,... n-1]. And each time, we split the current segment in half (assuming it hasn't already become a segment of length 1), run the identical operation on both halves, and then store the result for each such segment in the appropriate node.

Except for the last level, every level of the created segment tree will be fully filled. Additionally, since we always break each segment into two at every level, the tree will be a Full Binary Tree. There will always be n-1 internal nodes because the created tree is always a full binary tree with n leaves. Consequently, there will be 2*n - 1 nodes overall.

How tall is the segment tree for the supplied array?

The segment tree will be log2N in height. The amount of memory allotted for the segment tree will be (2 * 2log2n-1) since the tree must be represented using an array and the relationship between the parent and child indexes must be preserved.

Search for the Sum of a Range

How to calculate the sum using the segment tree once it has been built. The algorithm to calculate the sum of the elements is as follows.

int getSum(node, l, r) 
{
   if the range of the node is within l and r
        return value in the node
   else if the range of the node is completely outside l and r
        return 0
   else
    return getSum(node's left child, l, r) + 
           getSum(node's right child, l, r)
}

There are three situations in the aforementioned implementation that we need to address.

When traversing the tree, if the current node's range does not fall within the specified range, the value of that node was not added to the answer.
If the supplied range and the range of the node partially overlap, then move left or right in accordance with the overlap.
Add the range to the answer if the given range entirely overlaps it.

Update a value:

The update can be carried out recursively, just like tree building and query operations can. An outdated index has been provided to us. Let diff represent the new value. Beginning at the segment tree's root, we append diff to each node that has the specified index within its range. We don't modify a node if it doesn't have the specified index inside its range.

C++ Code

The application of the aforementioned strategy is seen below:

// C++ program to show segment tree operations like construction, query
// and update
#include <bits/stdc++.h>
using namespace std;

// A utility function to get the middle index from corner indexes.
int getMid(int s, int e) { return s + (e -s)/2; }

/* A recursive function to get the sum of values in the given range
	of the array. The following are parameters for this function.

	st --> Pointer to segment tree
	si --> Index of current node in the segment tree. Initially
			0 is passed as root is always at index 0
	ss & se --> Starting and ending indexes of the segment represented
				by current node, i.e., st[si]
	qs & qe --> Starting and ending indexes of query range */
int getSumUtil(int *st, int ss, int se, int qs, int qe, int si)
{
	// If segment of this node is a part of given range, then return
	// the sum of the segment
	if (qs <= ss && qe >= se)
		return st[si];

	// If segment of this node is outside the given range
	if (se < qs || ss > qe)
		return 0;

	// If a part of this segment overlaps with the given range
	int mid = getMid(ss, se);
	return getSumUtil(st, ss, mid, qs, qe, 2*si+1) +
		getSumUtil(st, mid+1, se, qs, qe, 2*si+2);
}

/* A recursive function to update the nodes which have the given
index in their range. The following are parameters
	st, si, ss and se are same as getSumUtil()
	i --> index of the element to be updated. This index is
			in the input array.
diff --> Value to be added to all nodes which have i in range */
void updateValueUtil(int *st, int ss, int se, int i, int diff, int si)
{
	// Base Case: If the input index lies outside the range of
	// this segment
	if (i < ss || i > se)
		return;

	// If the input index is in range of this node, then update
	// the value of the node and its children
	st[si] = st[si] + diff;
	if (se != ss)
	{
		int mid = getMid(ss, se);
		updateValueUtil(st, ss, mid, i, diff, 2*si + 1);
		updateValueUtil(st, mid+1, se, i, diff, 2*si + 2);
	}
}

// The function to update a value in input array and segment tree.
// It uses updateValueUtil() to update the value in segment tree
void updateValue(int arr[], int *st, int n, int i, int new_val)
{
	// Check for erroneous input index
	if (i < 0 || i > n-1)
	{
		cout<<"Invalid Input";
		return;
	}

	// Get the difference between new value and old value
	int diff = new_val - arr[i];

	// Update the value in array
	arr[i] = new_val;

	// Update the values of nodes in segment tree
	updateValueUtil(st, 0, n-1, i, diff, 0);
}

// Return sum of elements in range from index qs (query start)
// to qe (query end). It mainly uses getSumUtil()
int getSum(int *st, int n, int qs, int qe)
{
	// Check for erroneous input values
	if (qs < 0 || qe > n-1 || qs > qe)
	{
		cout<<"Invalid Input";
		return -1;
	}

	return getSumUtil(st, 0, n-1, qs, qe, 0);
}

// A recursive function that constructs Segment Tree for array[ss..se].
// si is index of current node in segment tree st
int constructSTUtil(int arr[], int ss, int se, int *st, int si)
{
	// If there is one element in array, store it in current node of
	// segment tree and return
	if (ss == se)
	{
		st[si] = arr[ss];
		return arr[ss];
	}

	// If there are more than one elements, then recur for left and
	// right subtrees and store the sum of values in this node
	int mid = getMid(ss, se);
	st[si] = constructSTUtil(arr, ss, mid, st, si*2+1) +
			constructSTUtil(arr, mid+1, se, st, si*2+2);
	return st[si];
}

/* Function to construct segment tree from given array. This function
allocates memory for segment tree and calls constructSTUtil() to
fill the allocated memory */
int *constructST(int arr[], int n)
{
	// Allocate memory for the segment tree

	//Height of segment tree
	int x = (int)(ceil(log2(n)));

	//Maximum size of segment tree
	int max_size = 2*(int)pow(2, x) - 1;

	// Allocate memory
	int *st = new int[max_size];

	// Fill the allocated memory st
	constructSTUtil(arr, 0, n-1, st, 0);

	// Return the constructed segment tree
	return st;
}

// Driver program to test above functions
int main()
{
	int arr[] = {1, 3, 5, 7, 9, 11};
	int n = sizeof(arr)/sizeof(arr[0]);

	// Build segment tree from given array
	int *st = constructST(arr, n);

	// Print sum of values in array from index 1 to 3
	cout<<"Sum of values in given range = "<<getSum(st, n, 1, 3)<<endl;

	// Update: set arr[1] = 10 and update corresponding
	// segment tree nodes
	updateValue(arr, st, n, 1, 10);

	// Find sum after the value is updated
	cout<<"Updated sum of values in given range = "
			<<getSum(st, n, 1, 3)<<endl;
	return 0;
}

Output:

Sum of values in given range = 15
Updated sum of values in given range = 22

Time complexity: O(N*log(N))
Auxiliary Space: O(N)

Next Topic2-3 Trees (Search, Insertion, and Deletion)

← prev next →

For Videos Join Our Youtube Channel: Join Now

Feedback

Send your Feedback to [email protected]

Help Others, Please Share

Learn Latest Tutorials

Splunk

SPSS

Swagger

Transact-SQL

Tumblr

ReactJS

Regex

Reinforcement Learning

R Programming

RxJS

React Native

Python Design Patterns

Python Pillow

Python Turtle

Keras

Preparation

Aptitude

Reasoning

Verbal Ability

Interview Questions

Company Questions

Trending Technologies

Artificial Intelligence

AWS

Selenium

Cloud Computing

Hadoop

ReactJS

Data Science

Angular 7

Blockchain

Git

Machine Learning

DevOps

B.Tech / MCA

DBMS

Data Structures

DAA

Operating System

Computer Network

Compiler Design

Computer Organization

Discrete Mathematics

Ethical Hacking

Computer Graphics

Software Engineering

Web Technology

Cyber Security

Automata

C Programming

C++

Java

.Net

Python

Programs

Control System

Data Mining

Data Warehouse

^{Like/Subscribe us for latest updates or newsletter}

DS Tutorial

DS Array

DS Linked List

DS Stack

DS Queue

DS Tree

DS Graph

DS Searching

DS Sorting

Differences

Misc

DS MCQ