Print a Binary Tree in Vertical Order

Print a binary tree vertically given one. The vertical order traversal is demonstrated in the example below.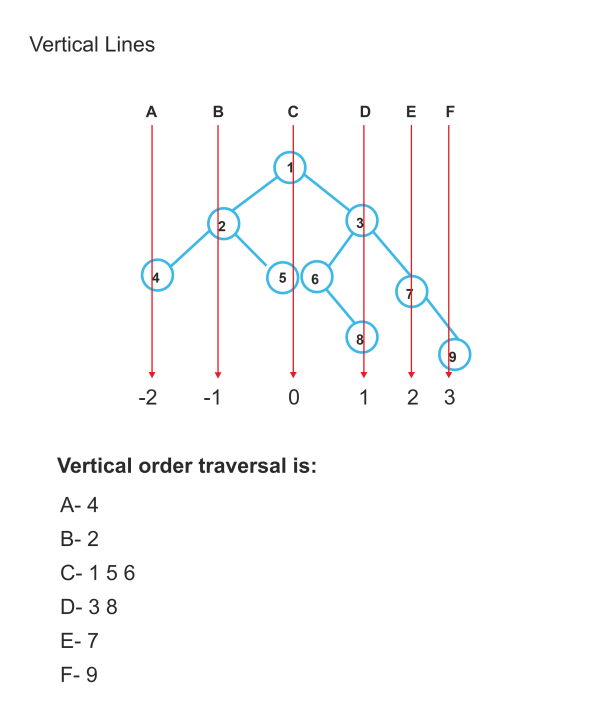

The goal is to make one pass through the tree and measure the minimum and maximum horizontal distances from the root. The smallest distance for the tree depicted above is -2 (for node with value 4), while the greatest distance is 3. (For node with value 9).

After determining the maximum and minimum distances from the root, we repeat for each vertical line from the minimum to the greatest distance from the root, walk the tree for each vertical line, and output the nodes that are along that vertical line.

Algorithm

Code in C++

The aforesaid algorithm is implemented as follows.

Output:

Vertical order traversal is 
4 
2 
1 5 6 
3 8 
7 
9 

Time Complexity: The aforementioned technique has an O(w*n) time complexity, where w is the width of the binary tree and n is the number of nodes. In the worst scenario, the value of w may be O(n) (take a whole tree as an example) and the time complexity could increase to O. (n2).

The method covered in this post can help tackle this issue more effectively. Soon, we'll talk about whole algorithms and how to put more effective techniques into practise.

Method -2 - More Optimized Method: (With MinHeaps)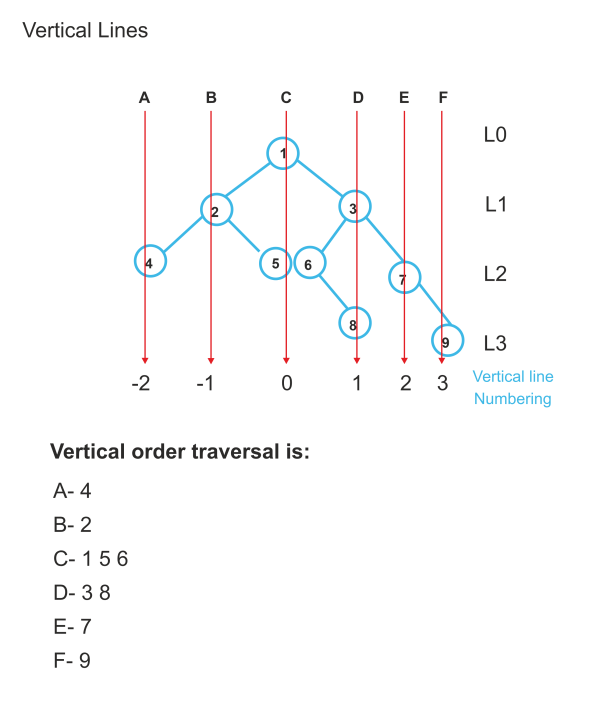

Algorithm

• So in this case, a tailored traversal is required.
• If we numerate the vertical lines in the manner shown in the image above.
• The Traversal in Ascending Order of Vertical Lines, the Ascending Order of Level, and the Traversal in Ascending Order of Level, IF SAME, are required.
• Thus, the four factors that we require are the Vertical Line Index, Level Index, Level Order Traversal (BFS) Number, and Node Value.
• Start with 0 at the root for vertical index numbering.
  • IF U GO LEFT, V = V - 1
  • IF u turn right, v = v+1. (View the diagram for a more detailed explanation of why it is.)
• Level Index = start with 0 in the root.
  • Just make l = l+1, as left or right we are going down only.
• Do level order traversal and save the poped nodes in the MINHEAP with the aforementioned change.
• Simply print it after you pop it from MINHEAP.
• When you reach the subsequent vertical line, print a newline if necessary.

NOTE:

• MinHeap, why? As we need Ascending order, minimum thing first at the top.
• we used pair<pair<int,int>,pair<int,int>> to store all 4 paratmeters {{ },{ }}

Code in C++

The aforesaid algorithm is implemented as follows.

Output:

Vertical order traversal is 
4 
2 
1 5 6 
3 8 
7 
9 

Time Complexity: O(N*LogN) Time

Reason:

• Normal Level Order (BFS) Traversal takes O(N).
• But here we are pushing into MinHeap - Single push O(LogN).
• So Overall O(N*LogN).
• Also while popping out from minHeap O(N*LogN).

Auxiliary Space: O(N)

Reason:

• The queue will have max at Last Level O(N/2) = O(N).
• The heap also stores all the nodes at a point, so O(N).

N is the Size of the Binary Tree. (Total no. of nodes)