Weight Balanced Binary TreeIn the domain of computer science and data structures, the effective organization and retrieval of data pose several challenges. Binary trees, in their large manifestations, assume an important role in data storage and retrieval. In this text, we will focus upon a specific binary tree also known as a "Weight Equilibrated Binary Tree" and understand its configuration, functionalities, merits, and execution. 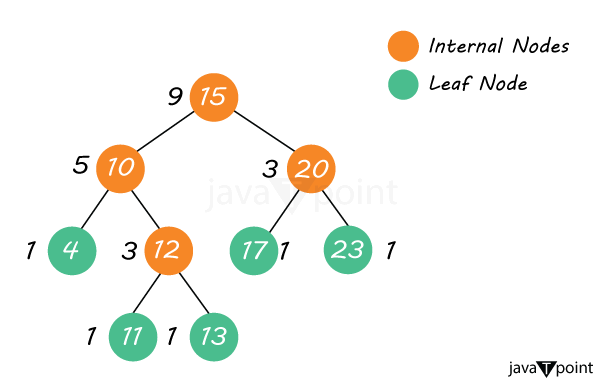
Initiation to Weight Equilibrated Binary TreesBinary trees are hierarchical data constructs comprising nodes, where each node maybe nil, one, or dual progeny. The equilibrium of a binary tree refers to the way of nodes on its left and right substructures. Achieving the equilibrium is important for the enhancement of actions like exploration, creation, and deletion. Weight Equilibrated Binary Tree ConstituentsA Weight Equilibrated Binary Tree is a distinctive subtype of binary tree that is devoted to sustaining equilibrium predicated on the magnitude or size of its substructures. In a weight equilibrated binary tree, the divergence in the tally of nodes between the left and right substructures is kept within well-defined thresholds, ensuring the tree's constancy. Weight equilibrated binary trees exhibit differentiation from other classes of binary trees, including AVL trees and Red-Black trees, which predominantly realign themselves contingent on the stature of the tree. Operational Procedures in Weight Equilibrated Binary TreesIn the event of appending or obliterating nodes in a weight equilibrated binary tree, the structure is realigned to ensure the preservation of the weight equilibrium attribute. This involves maneuvers and rectification operations, akin to those witnessed in other self-adjusting binary trees. Equilibrium Strategies Weight equilibrated binary trees deploy a panoply of equilibrating methodologies to sustain the desired weight equilibrium, such as leftward and rightward revolutions and reorganization. These maneuvers are meticulously contrived to downsize tree imbalances and optimize the retrieval of data. Merits and ApplicationsWeight equilibrated binary trees offer a number of benefits. They show efficiency in functions like exploration, addition, and subtraction, rendering them invaluable for scenarios necessitating the management of dynamic data. Use cases use systems for the governance of databases, precedence queues, and repositories. Code: Let's take a look at a simple Python code snippet for implementing a weight balanced binary tree: Output: Node with value 8 found. Tips for Efficient ImplementationA proficient realization of weight-balanced binary trees necessitates an exhaustive comprehension of the equilibrium algorithms. The selection of an apt data structure and the meticulous upkeep of precise weight tallies for subtrees stand as important facets for the execution of this system. 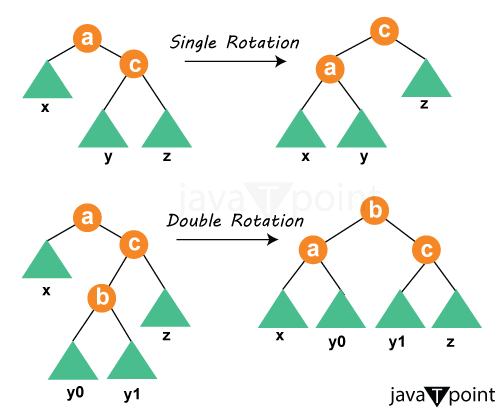
Comparing Other Data Structures with Weight Balanced Binary TreesWeight-balanced binary trees exhibit complex attributes, circling both their strengths and weaknesses. They work as required when confronted with scenarios like insertions and deletions. However, it's worth noting that alternative data structures, such as AVL trees and Red-Black trees, may eclipse them in diverse utilization situations. Comprehending these intricate trade-offs becomes imperative when the time comes to elect the most fitting data structure for a specific application. ConclusionIn the domain of data structure management, Weight Balanced Binary Trees emerge as a sophisticated solution for preserving equilibrium within binary tree structures, particularly in scenarios demanding dynamic data manipulation. Their distinct methodology of balance maintenance, rooted in the assessment of subtree weights, distinguishes them from their self-balancing counterparts. When faced with the pivotal decision of selecting an appropriate data structure, it becomes imperative to meticulously assess the precise requisites of your application, thus enabling a judicious choice.
Next TopicTransform a BST to greater sum tree
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share









