Construct Tree from Given Inorder and Preorder Traversals

Introduction:

Tree traversal algorithms are fundamental in understanding and reconstructing binary trees. Given the Inorder and Preorder traversals of a binary tree, it is possible to reconstruct the original tree. This process involves utilizing the properties of these traversals to rebuild the tree structure accurately.

Understanding Inorder and Preorder Traversals:

Inorder and Preorder traversals are methods used to explore and display nodes in a binary tree.

Inorder Traversal

In an inorder traversal, we visit the left subtree, then the root, and finally the right subtree.

For a binary tree, the inorder traversal produces a sorted sequence of node values.

Preorder Traversal

In a preorder traversal, we visit the root, then the left subtree, and finally the right subtree.

The preorder traversal is crucial for reconstructing the tree structure.

Consider the following binary tree: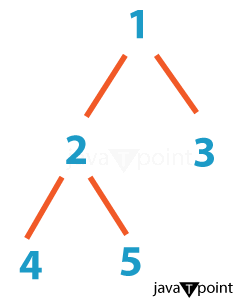

The inorder traversal of this tree would be 4-2-5-1-3, and the preorder traversal would be 1-2-4-5-3.

Reconstruction Process:

Given the Inorder and Preorder traversals, it is possible to reconstruct the original binary tree. The key lies in understanding the characteristics of each traversal method and their relationship to the tree structure.

Here are the steps to construct a binary tree from the Inorder and Preorder traversals:

Steps:

• Identify the Root: In Preorder traversal, the first element encountered is always the root node.
• Locate Root in Inorder Traversal: Using the value obtained from the previous step (the root node), find its index in the Inorder traversal. This index separates the left and right subtrees in Inorder.
• Recursion for Subtrees: Based on the index found in the Inorder traversal, we can determine the size of left and right subtrees. Recursively repeat the above steps for left and right subtrees.

Step-by-Step Construction with Example:

Let's consider the inorder and preorder traversals for a binary tree:

Inorder: [D, B, E, A, F, C]

Preorder: [A, B, D, E, C, F]

• Select the Root:

The root is 'A' (first element in the preorder traversal).

• Find Root in Inorder:

'A' is at position 3 in the inorder traversal.

• Recursively Construct Left and Right Subtrees:

For the left subtree: Inorder [D, B, E], Preorder [B, D, E]

For the right subtree: Inorder [F, C], Preorder [C, F]

Repeat the process for each subtree until the entire tree is constructed.

Implementation:

Explanation:

• The binary tree is defined using a TreeNode struct, and the construction logic is implemented in the Solution class.
• In the Solution class, the buildTree method is responsible for initiating the construction process. It takes two vectors as input parameters: preorder, representing the preorder traversal of the binary tree, and inorder, representing the inorder traversal.
• The method utilizes an unordered map called indexMap to efficiently store the indices of elements in the inorder traversal for quick lookup during the tree construction process.
• The actual construction of the binary tree is performed by the buildTreeHelper method, a recursive function that takes the current segments of the preorder and inorder traversals, along with the index map.
• This helper function constructs the root node of the current subtree using the first element in the preorder traversal.
• It then determines the size of the left subtree by finding the index of the root value in the inorder sequence. Recursively, the left and right subtrees are constructed based on the corresponding segments of the traversals.
• The inorderTraversal function is used for validation, performing an inorder traversal of the constructed tree.
• In the main function, an instance of the Solution class is created, and the buildTree method is called with example preorder and inorder traversals.
• The constructed binary tree's inorder traversal is then printed to the console, validating that the tree has been correctly built.

Program Output:

Optimized Recursive Solution with Hashing:

To optimize the above recursive solution, we can use a hash table to store the indices of elements in the inorder traversal. This eliminates the need for linear search to find the root's position in the inorder traversal.

Explanation:

• The binary tree is represented using a struct TreeNode, which has an integer value, a left child pointer (left), and a right child pointer (right).
• The main function buildTree takes two vectors as input: preorder representing the preorder traversal of the binary tree, and inorder representing the inorder traversal.
• The function constructs and returns the binary tree based on these traversals. It uses a helper function buildTreeHelper that recursively builds the tree using the indices and mappings provided by the input vectors.
• The buildTreeHelper function takes the current range of indices for the preorder and inorder traversals (preStart, preEnd, inStart, inEnd) and a map (inorderMap) that stores the mapping of values to their indices in the inorder traversal.
• The base case checks if the range is invalid, in which case it returns nullptr. Otherwise, it creates a new node with the value from the current preorder index (preStart) and recursively builds its left and right subtrees based on the calculated indices.
• The printInorder function is a simple utility function to perform an inorder traversal of the constructed binary tree and print the values to the console. It is used in the main function to display the inorder traversal of the constructed tree.
• In the main function, two example vectors preorder and inorder are provided to demonstrate the usage of the buildTree
• The constructed tree is printed using the printInorder function, showing the inorder traversal of the binary tree.

Program Output:

Conclusion:

In conclusion, the problem of constructing a tree from given inorder and preorder traversals is a classic computer science challenge that involves reconstructing a binary tree based on the provided orderings of its nodes.

The inorder traversal depicts the sequence in which the nodes are visited, while the preorder traversal provides the root-first exploration order. Solving this problem requires a systematic approach to identify the root, left, and right subtrees, allowing for the reconstruction of the original binary tree.

One key observation is that the first element in the preorder traversal is always the root of the tree. By locating this root in the inorder traversal, we can determine the positions of the left and right subtrees. This insight forms the basis of a recursive algorithm to construct the entire binary tree. As the algorithm progresses, it subdivides the problem into smaller subproblems until the entire tree is reconstructed. This recursive approach takes advantage of the inherent structure in the traversals and efficiently reconstructs the binary tree with a time complexity proportional to the number of nodes.