Shell Sort AlgorithmIn this article, we will discuss the shell sort algorithm. Shell sort is the generalization of insertion sort, which overcomes the drawbacks of insertion sort by comparing elements separated by a gap of several positions. It is a sorting algorithm that is an extended version of insertion sort. Shell sort has improved the average time complexity of insertion sort. As similar to insertion sort, it is a comparison-based and in-place sorting algorithm. Shell sort is efficient for medium-sized data sets. In insertion sort, at a time, elements can be moved ahead by one position only. To move an element to a far-away position, many movements are required that increase the algorithm's execution time. But shell sort overcomes this drawback of insertion sort. It allows the movement and swapping of far-away elements as well. This algorithm first sorts the elements that are far away from each other, then it subsequently reduces the gap between them. This gap is called as interval. This interval can be calculated by using the Knuth's formula given below - Now, let's see the algorithm of shell sort. AlgorithmThe simple steps of achieving the shell sort are listed as follows - Working of Shell sort AlgorithmNow, let's see the working of the shell sort Algorithm. To understand the working of the shell sort algorithm, let's take an unsorted array. It will be easier to understand the shell sort via an example. Let the elements of array are - 
We will use the original sequence of shell sort, i.e., N/2, N/4,....,1 as the intervals. In the first loop, n is equal to 8 (size of the array), so the elements are lying at the interval of 4 (n/2 = 4). Elements will be compared and swapped if they are not in order. Here, in the first loop, the element at the 0th position will be compared with the element at 4th position. If the 0th element is greater, it will be swapped with the element at 4th position. Otherwise, it remains the same. This process will continue for the remaining elements. At the interval of 4, the sublists are {33, 12}, {31, 17}, {40, 25}, {8, 42}. 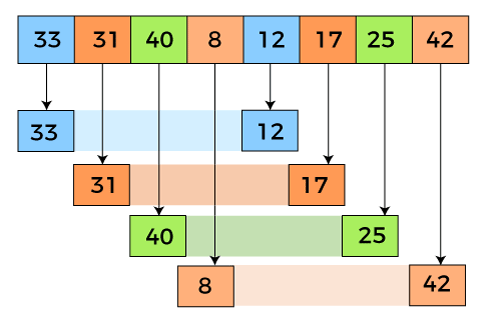
Now, we have to compare the values in every sub-list. After comparing, we have to swap them if required in the original array. After comparing and swapping, the updated array will look as follows - 
In the second loop, elements are lying at the interval of 2 (n/4 = 2), where n = 8. Now, we are taking the interval of 2 to sort the rest of the array. With an interval of 2, two sublists will be generated - {12, 25, 33, 40}, and {17, 8, 31, 42}. 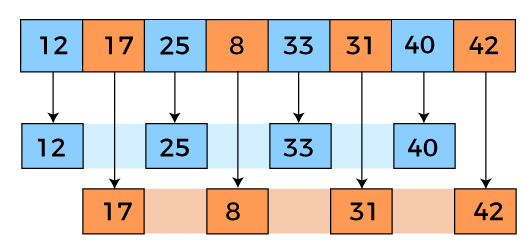
Now, we again have to compare the values in every sub-list. After comparing, we have to swap them if required in the original array. After comparing and swapping, the updated array will look as follows - 
In the third loop, elements are lying at the interval of 1 (n/8 = 1), where n = 8. At last, we use the interval of value 1 to sort the rest of the array elements. In this step, shell sort uses insertion sort to sort the array elements. 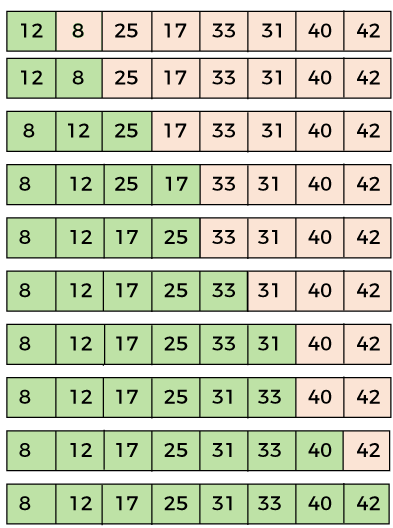
Now, the array is sorted in ascending order. Shell sort complexityNow, let's see the time complexity of Shell sort in the best case, average case, and worst case. We will also see the space complexity of the Shell sort. 1. Time Complexity
2. Space Complexity
Implementation of Shell sortNow, let's see the programs of Shell sort in different programming languages. Program: Write a program to implement Shell sort in C language. Output After the execution of above code, the output will be - 
Program: Write a program to implement Shell sort in C++. Output After the execution of the above code, the output will be - 
Program: Write a program to implement Shell sort in C#. Output After the execution of the above code, the output will be - 
Program: Write a program to implement Shell sort in Java. Output After the execution of the above code, the output will be - 
So, that's all about the article. Hope the article will be helpful and informative to you.
Next TopicBitonic Sort
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share









