Minimum Insertions to form a Palindrome

What is a Palindrome?

If a string is read from the backward and forward direction as the same then the string is known as a palindrome string.

The reverse of the palindrome string is the same as the string.

For example:

"abcddbca", "abcdbca" are an example of palindrome strings.

Problem statement:

Here, we are given an input string, and we have to return the minimum number of characters inserted at any position of the given string so that the given string becomes a palindrome string.

For example:

The string is "abcd", and we will require three insertions to form a palindrome string.

The resulting string will be "abcdcba". If the string is "abcba", we will require 0 insertions as it is already a palindrome.

Method 1

We will use a recursive approach to solve the problem. Our task is to determine the minimum number of insertions for the string, which is defined from the index 0 to index n-1 where n is the length of the string.

So string will be represented as str[low, hi]

There are two cases:

Case 1: If str[low]==str[hi] then we will get answer from str[llow+1,hi-1]

Case 2: Otherwise we will get the answer as Minimum(str[low,hi-1],str[low+1,hi])+1.

Java code:

Output:

Explanation

In the above code, we have a string as "abcdba", which is not a palindrome. We will require only one insertion of character 'c' to make it a palindrome.

The resulting string is "abcdcba", which is a palindrome string.

The time complexity of the above code: is O(nⁿ ), which is exponential.

Space complexity: O(n) for recursion stack space.

Method 2

The above recursive code has an overlapping sub-array problem, so we can optimize any recursive problem using the dynamic programming approach which has an overlapping sub array problem.

We will use memoization techniques (It is an optimization technique in programming that makes applications more efficient and hence faster) to solve the problem. In memoization, we will store the result of every recursive call into an array, so we don't calculate again next time.

Java code:

Output:

Explanation

In the above code, we have a string as "abcdca", which requires character 'b' to make itself a palindrome. So, the answer is one, and we use a 2d array of nxn to store the result of every recursive call.

Time complexity: O(n²)

Space complexity: O(n²)+recursion stack space

We can further optimize it without using the recursion. We can use the tabulation method and avoid the extra space used by the recursion.

Method 3

We will use a 2D array where dp[i][j] will store the minimum characters needed to make a palindrome of string from the i^th index to the j^th index.

We will use the gap method where the gap will start from 0 to n-1, and we will fill the table gap-wise.

Java code:

Output:

In the above code, we have a string as "abcdef", which will require at least five characters to form a palindrome string which will be "abcdefedcba".

Time complexity: O(n²)

Space complexity: O(n²)

Method 4

This is one of the most popular approaches to solve this problem.

If we get the length of the longest palindrome subsequence of the given string, then the number of remaining characters will make our answer.

If we get the longest common subsequence of the string with its reverse string, then it will return the length of the longest palindrome subsequence.

Let L is the longest palindrome subsequence length, and then n-L is the answer.

For example: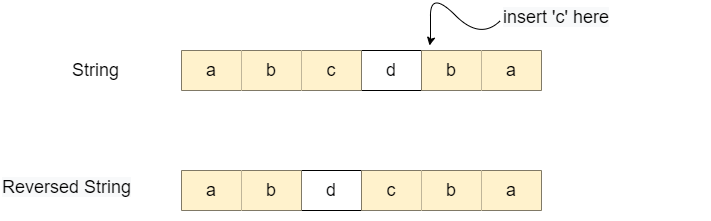

Java code:

Output:

Explanation

We find the longest common subsequence of string and its reverse string, and we get our resultant value.

Time complexity: O(n2)

Space complexity: O(n2)