Find whether an array is subset of another array

Two arrays, arr1[0..m-1] and arr2[0..n-1], are provided. Determine whether or whether arr2[] is a subset of arr1[]. The two arrays are not ordered in any way. It is possible to assume that each element in both arrays is unique.

EXAMPLES

Example-1

Output:

arr2[] is a subset of arr1[]

Example-2

Output:

arr2[] is a subset of arr1[]

Example-3

Output:

arr2[] is not a subset of arr1[]

Simple Way to Check whether One Array Is a Subset of Another Array

Utilize two loops: The outer loop selects each member of arr2[] individually. The element chosen by the outer loop is looked for linearly by the inner loop. Return 1 if all elements were located; otherwise, return 0.

The application of the aforementioned strategy is seen below:

CODE

// C++ program to find whether an array
// is subset of another array
#include <bits/stdc++.h>

/* Return 1 if arr2[] is a subset of
arr1[] */
bool isSubset(int arr1[], int arr2[], int m, int n)
{
	int i = 0;
	int j = 0;
	for (i = 0; i < n; i++) {
		for (j = 0; j < m; j++) {
			if (arr2[i] == arr1[j])
				break;
		}

		/* If the above inner loop was
		not broken at all then arr2[i]
		is not present in arr1[] */
		if (j == m)
			return 0;
	}

	/* If we reach here then all
	elements of arr2[] are present
	in arr1[] */
	return 1;
}

// Driver code
int main()
{
	int arr1[] = { 11, 1, 13, 21, 3, 7 };
	int arr2[] = { 11, 3, 7, 1 };

	int m = sizeof(arr1) / sizeof(arr1[0]);
	int n = sizeof(arr2) / sizeof(arr2[0]);

	if (isSubset(arr1, arr2, m, n))
		printf("arr2[] is subset of arr1[] ");
	else
		printf("arr2[] is not a subset of arr1[]");

	getchar();
	return 0;
}

Output:

arr2[] is subset of arr1[]

Complexity of Time : O(m*n)

Complexity of Space: O(1)

Utilize sorting and binary search to determine whether one array is a subset of another array.

The plan is to sort the provided array arr1[] before conducting a binary search for each member in arr2[] in the sorted arr1[]. Return 0 if the element cannot be found. Return 1 if all elements are present.

Illustration:

Given array arr1[] = { 11, 1, 13, 21, 3, 7 } and arr2[] = { 11, 3, 7, 1 }.

Step 1: We will sort the array arr1[], and have arr1[] = { 1, 3, 7, 11, 13, 21}.

Step 2: We will look for each element in arr2[] in arr1[] using binary search.

arr2[] = { 11, 3, 7, 1 }, 11 is present in arr1[] = { 1, 3, 7, 11, 13, 21}
arr2[] = { 11, 3, 7, 1 }, 11 is present in arr1[] = { 1, 3, 7, 11, 13, 21}
arr2[] = { 11, 3, 7, 1 }, 11 is present in arr1[] = { 1, 3, 7, 11, 13, 21}
arr2[] = { 11, 3, 7, 1 }, 11 is present in arr1[] = { 1, 3, 7, 11, 13, 21}

As all the elements are found we can conclude arr2[] is the subset of arr1[].

Algorithm:

The algorithm is rather easy to understand.

The first array, arr1, is sorted.
Search sorted arr1[ for the components of arr2[].
The code will be terminated if we come across a specific value that is present in arr2[] but not in arr1[; arr2[] can never be the subset of arr1[].
If not, arr1[ is a subset of arr2[].

The above method is implemented with the following code:

CODE

// C++ program to find whether an array
// is subset of another array
#include <bits/stdc++.h>
using namespace std;

/* Function prototypes */
void quickSort(int* arr, int si, int ei);
int binarySearch(int arr[], int low, int high, int x);

/* Return 1 if arr2[] is a subset of arr1[] */
bool isSubset(int arr1[], int arr2[], int m, int n)
{
	int i = 0;

	quickSort(arr1, 0, m - 1);
	for (i = 0; i < n; i++) {
		if (binarySearch(arr1, 0, m - 1, arr2[i]) == -1)
			return 0;
	}

	/* If we reach here then all elements
	of arr2[] are present in arr1[] */
	return 1;
}

/* FOLLOWING FUNCTIONS ARE ONLY FOR
	SEARCHING AND SORTING PURPOSE */
/* Standard Binary Search function*/
int binarySearch(int arr[], int low, int high, int x)
{
	if (high >= low) {
		/*low + (high - low)/2;*/
		int mid = (low + high) / 2;

		/* Check if arr[mid] is the first
		occurrence of x. arr[mid] is first
		occurrence if x is one of the following
		is true:
		(i) mid == 0 and arr[mid] == x
		(ii) arr[mid-1] < x and arr[mid] == x */
		if ((mid == 0 || x > arr[mid - 1])
			&& (arr[mid] == x))
			return mid;
		else if (x > arr[mid])
			return binarySearch(arr, (mid + 1), high, x);
		else
			return binarySearch(arr, low, (mid - 1), x);
	}
	return -1;
}

void exchange(int* a, int* b)
{
	int temp;
	temp = *a;
	*a = *b;
	*b = temp;
}

int partition(int A[], int si, int ei)
{
	int x = A[ei];
	int i = (si - 1);
	int j;

	for (j = si; j <= ei - 1; j++) {
		if (A[j] <= x) {
			i++;
			exchange(&A[i], &A[j]);
		}
	}
	exchange(&A[i + 1], &A[ei]);
	return (i + 1);
}

/* Implementation of Quick Sort
A[] --> Array to be sorted
si --> Starting index
ei --> Ending index
*/
void quickSort(int A[], int si, int ei)
{
	int pi; /* Partitioning index */
	if (si < ei) {
		pi = partition(A, si, ei);
		quickSort(A, si, pi - 1);
		quickSort(A, pi + 1, ei);
	}
}

/*Driver code */
int main()
{
	int arr1[] = { 11, 1, 13, 21, 3, 7 };
	int arr2[] = { 11, 3, 7, 1 };

	int m = sizeof(arr1) / sizeof(arr1[0]);
	int n = sizeof(arr2) / sizeof(arr2[0]);

	if (isSubset(arr1, arr2, m, n))
		cout << "arr2[] is subset of arr1[] ";
	else
		cout << "arr2[] is not a subset of arr1[] ";

	return 0;
}

Output:

arr2[] is subset of arr1[]

Complexity of Time : O(nlog (m) + mLog (m)). Sorting takes O(mLog(m)) and binary searching over every element of one array in another takes O(nlog(m)). Quick Sort is used in the code above, and its worst-case time complexity is O. (m²).

Complexity of Space: O(n)

Utilize sorting and merging to determine if one array is a subset of another array.

The plan is to sort the two arrays before utilising two pointers to iteratively search the second array for identical values from the first array. Every time we come across the same values, we increase the value of the pointer pointing to both arrays, and if we come across any values that are lower than those of the second array, we increase the value of the pointer pointing to the first array. We know the second array is not a subset of the first array if the value is higher than that of the second array.

Illustration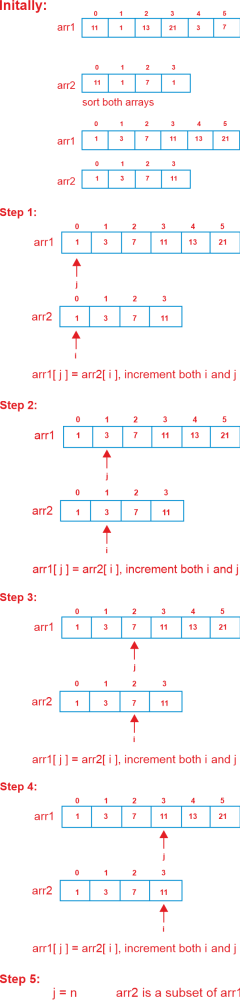

Find whether an array is subset of another array

Algorithm:

The two arrays will first need to be sorted.

A pair of pointers, j and I or arr1[] and arr2[], should be set.
In this case, we shall raise j by 1 if arr1[j] arr2[i].
Increase j and I by 1 if arr1[j] = arr2[i].
We will stop because arr2[] is not a subset of arr1[] if arr1[j] > arr2[i].

The application of the aforementioned strategy is seen below:

CODE

// C++ program to find whether an array
// is subset of another array
#include <bits/stdc++.h>
using namespace std;

/* Return 1 if arr2[] is a subset of arr1[] */
bool isSubset(int arr1[], int arr2[], int m, int n)
{
	int i = 0, j = 0;

	if (m < n)
		return 0;

	// Sort both the arrays
	sort(arr1, arr1 + m);
	sort(arr2, arr2 + n);

	// Iterate till they do not exceed their sizes
	while (i < n && j < m) {
		// If the element is smaller then
		// Move ahead in the first array
		if (arr1[j] < arr2[i])
			j++;
		// If both are equal, then move
		// both of them forward
		else if (arr1[j] == arr2[i]) {
			j++;
			i++;
		}

		// If we do not have an element smaller
		// or equal to the second array then break
		else if (arr1[j] > arr2[i])
			return 0;
	}

	return (i < n) ? false : true;
}

// Driver Code
int main()
{
	int arr1[] = { 11, 1, 13, 21, 3, 7 };
	int arr2[] = { 11, 3, 7, 1 };

	int m = sizeof(arr1) / sizeof(arr1[0]);
	int n = sizeof(arr2) / sizeof(arr2[0]);

	if (isSubset(arr1, arr2, m, n))
		printf("arr2[] is subset of arr1[] ");
	else
		printf("arr2[] is not a subset of arr1[] ");

	return 0;
}

Output:

arr2[] is subset of arr1[]

Complexity of Time : O(mLog(m) + nLog(n)) which is better than approach 2.

Complexity of Space: O(1)

Utilize hashing to determine whether an array is a subset of another array.

The concept is to place every element from the first array into a HashSet, iterate through the second array to see if the element is there, and if not, determine whether the second array is a subset of the first array.

Illustration:

Given array arr1[] = { 11, 1, 13, 21, 3, 7 } and arr2[] = { 11, 3, 7, 1 }.

Step 1: We will store the array arr1[] elements in HashSet

Step 2: We will look for each element in arr2[] in arr1[] using binary search.

arr2[] = { 11, 3, 7, 1 }, 11 is present in the HashSet = { 1, 3, 7, 11, 13, 21}
arr2[] = { 11, 3, 7, 1 }, 3 is present in the HashSet = { 1, 3, 7, 11, 13, 21}
arr2[] = { 11, 3, 7, 1 }, 7 is present in the HashSet = { 1, 3, 7, 11, 13, 21}
arr2[] = { 11, 3, 7, 1 }, 1 is present in the HashSet = { 1, 3, 7, 11, 13, 21}

As all the elements are found we can conclude arr2[] is the subset of arr1[].

Algorithm:

The algorithm is rather easy to understand.

In a HashSet, save the first array arr1[].
Search the HashSet for the elements of arr2[].
The code will exit if we come across a certain value that is present in arr2[] but not in the HashSet since arr2[] can never be a subset of arr1[.
If not, arr1[ is a subset of arr2[].

The application of the aforementioned strategy is seen below:

CODE

// C++ code to find whether an array is subset of
// another array
#include <bits/stdc++.h>
using namespace std;

/* Return true if arr2[] is a subset of arr1[] */
bool isSubset(int arr1[], int m, int arr2[], int n)
{

	// Using STL set for hashing
	set<int> hashset;

	// hset stores all the values of arr1
	for (int i = 0; i < m; i++) {
		hashset.insert(arr1[i]);
	}

	// loop to check if all elements of arr2 also
	// lies in arr1
	for (int i = 0; i < n; i++) {
		if (hashset.find(arr2[i]) == hashset.end())
			return false;
	}
	return true;
}

// Driver Code
int main()
{
	int arr1[] = { 11, 1, 13, 21, 3, 7 };
	int arr2[] = { 11, 3, 7, 1 };
	int m = sizeof(arr1) / sizeof(arr1[0]);
	int n = sizeof(arr2) / sizeof(arr2[0]);

	if (isSubset(arr1, m, arr2, n))
		cout << "arr2[] is subset of arr1[] "
			<< "\n";
	else
		cout << "arr2[] is not a subset of arr1[] "
			<< "\n";
	return 0;
}

Output:

arr2[] is subset of arr1[]

Complexity of Time : O(nLog(n))

Complexity of Space: O(n)

Using Set, determine whether one array is a subset of another array.

The goal is to include every member from both the first and second arrays in the set; if the set's size is the same as arr1[], then arr2[] is a subset of arr1[. Since arr2[] contains no newly discovered elements, the subset is.

Illustration:

Given array arr1[] = { 11, 1, 13, 21, 3, 7 } and arr2[] = { 11, 3, 7, 1 }.

Step 1: We will store the array arr1[] and arr2[] elements in Set

The final Set = { 1, 3, 7, 11, 13, 21}

Step 2: Size of arr1[] = 6 and size of the Set = 6

Hence no new elements are found in arr2[]

As all the elements are found we can conclude arr2[] is the subset of arr1[].

Algorithm:

The algorithm is rather easy to understand.

Set up the first array, arr1[].
The first array arr1[] should be kept in the same Set.
Arr2[] is the subset of arr1[] if the size of arr1[] equals the size of the Set.
If not, arr1[] and arr2[] are not its subset.

CODE

#include <bits/stdc++.h>
using namespace std;

int main()
{
	// code
	int arr1[] = { 11, 1, 13, 21, 3, 7 };
	int arr2[] = { 11, 3, 7, 1 };
	int m = sizeof(arr1) / sizeof(arr1[0]);
	int n = sizeof(arr2) / sizeof(arr2[0]);
	unordered_set<int> s;
	for (int i = 0; i < m; i++) {
		s.insert(arr1[i]);
	}
	int p = s.size();
	for (int i = 0; i < n; i++) {
		s.insert(arr2[i]);
	}
	if (s.size() == p) {
		cout << "arr2[] is subset of arr1[] "
			<< "\n";
	}
	else {
		cout << "arr2[] is not subset of arr1[] "
			<< "\n";
	}
	return 0;
}

Output:

arr2 [] is subset of arr1 []

Given array arr1 [] = { 11, 1, 13, 21, 3, 7 } and arr2 [] = { 11, 3, 7, 1 }.

Step 1: We will store the array arr1[] elements frequency in the frequency array

The frequency array will look like this

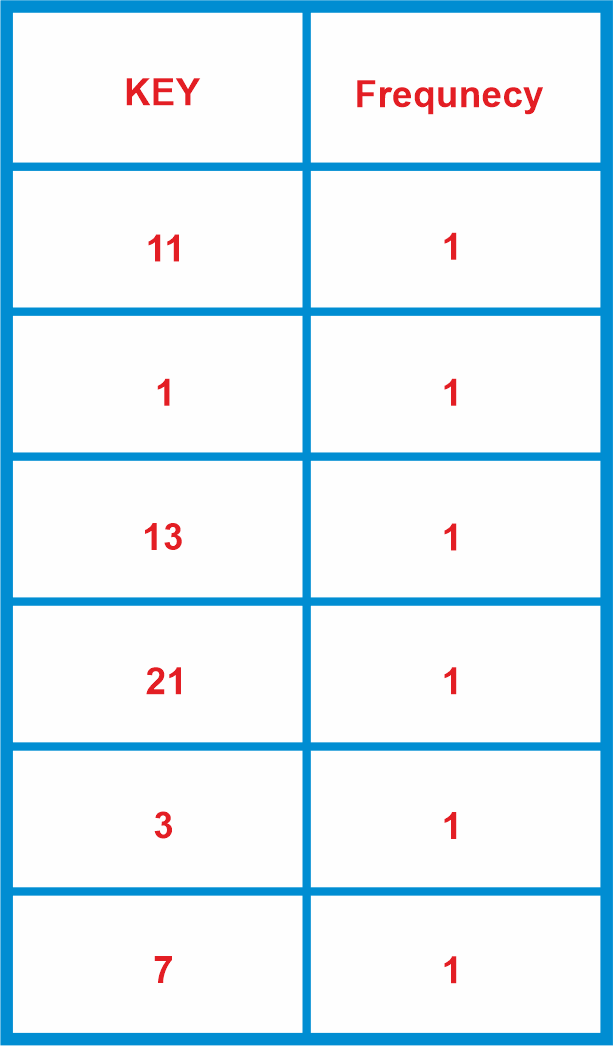
Step 2: We will look for arr2[] elements in the frequnecy array.

arr2[] = { 11, 3, 7, 1 }, 11 is present in the Frequnecy array
arr2[] = { 11, 3, 7, 1 }, 3 is present in the Frequnecy array
arr2[] = { 11, 3, 7, 1 }, 7 is present in the Frequnecy array
arr2[] = { 11, 3, 7, 1 }, 1 is present in the Frequnecy array

As all the elements are found we can conclude arr2[] is the subset of arr1[].

Algorithm:

The algorithm is rather easy to understand.

The frequency array should be used to store the frequency of the initial array elements of arr1 [].
Search the frequency array for the elements of the arr2[] iteration.
Reduce the frequency value by one if the value is present in the frequency array.
We will conclude that arr2[] is not a subset of arr1[] if any element in arr2[] has a frequency of less than 1.

The application of the aforementioned strategy is seen below:

CODE

// C++ program to find whether an array
// is subset of another array
#include <bits/stdc++.h>
using namespace std;
/* Return true if arr2[] is a subset of arr1[] */

bool isSubset(int arr1[], int m, int arr2[], int n)
{
	// Create a Frequency Table using STL
	map<int, int> frequency;

	// Increase the frequency of each element
	// in the frequency table.
	for (int i = 0; i < m; i++) {
		frequency[arr1[i]]++;
	}
	// Decrease the frequency if the
	// element was found in the frequency
	// table with the frequency more than 0.
	// else return 0 and if loop is
	// completed return 1.
	for (int i = 0; i < n; i++) {
		if (frequency[arr2[i]] > 0)
			frequency[arr2[i]]--;
		else {
			return false;
		}
	}
	return true;
}

// Driver Code
int main()
{
	int arr1[] = { 11, 1, 13, 21, 3, 7 };
	int arr2[] = { 11, 3, 7, 1 };
	int m = sizeof(arr1) / sizeof(arr1[0]);
	int n = sizeof(arr2) / sizeof(arr2[0]);

	if (isSubset(arr1, m, arr2, n))
		cout << "arr2[] is subset of arr1[] "
			<< "\n";
	else
		cout << "arr2[] is not a subset of arr1[] "
			<< "\n";
	return 0;
}

Output:

arr2[] is subset of arr1[]

Complexity of Time : O(m+n) which is better than methods 1,2,3

Complexity of Space: O(n)

Be aware that methods 1, 2, 4, and 5 do not address the situation where we have duplicates in arr2[]. For instance, these methods will output 1, 4, 4, 2, even though it is not a subset of 1, 4, 2.

Next TopicPrint a Binary Tree in Vertical Order

← prev next →