B Tree Insertion

The following tutorial will discuss how to insert a key into a B Tree. Moreover, we will see some working examples of inserting keys into a B Tree in different programming languages like C, C++, Java, and Python.

But before we get started, let us briefly recall the B Tree data structure and its properties.

What is a B Tree?

B Tree is an example of a Self-Balancing Binary Search Tree data structure that stores and maintains data in a sorted form where the left child nodes of the root are smaller than the root node and the right child nodes are larger than the root node in value. The B Tree data structure allows programmers to search data in an efficient way and process different operations in logarithmic time. It also allows nodes to have more than two children. Every node of the B Tree stores the key value along with the data pointer pointing to the block in the disk file consisting of that key. B Trees are generally utilized for the implementation of multilevel indexing.

Let us now understand some important properties of a B Tree.

Properties of B Tree

The following are some important properties of a B Tree:

1. Every node has at most m children, where m is the order of the B Tree.
2. A node having K children consists of K-1 keys.
3. Every non-leaf node, excluding the root node, must have at least [m/2] child nodes.
4. The root node must have at least two children if it is not the leaf node.
5. Unlike the other trees, the height of a B Tree increases upwards toward the root node, and the insertion happens at the leaf node.
6. The Time Complexity of all the operations of a B Tree is O(log?n), where 'n' is the number of data elements present in the B Tree.

The following is an example of a B Tree of order 4: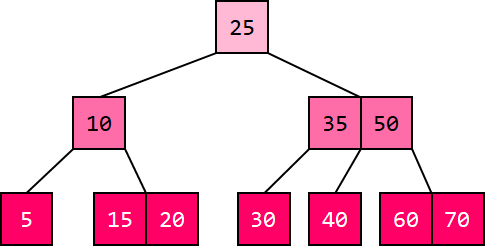

Figure 1: A B Tree of order 4

Let us now learn how the insertion works in a B Tree.

Insertion Operation in a B Tree

Insertion of a data element in a B Tree contains two main events:

1. Searching for the appropriate node where the element will be inserted.
2. Splitting of the node, if required.

The Insertion Operation always follows the Bottom-Up approach.

Let us understand these events below:

Step 1: If the Tree is empty, a root node is allocated, and we will insert the key.

Step 2: We will then update the allowed number of keys in the node.

Step 3: We will then search for the appropriate node for the insertion of the element.

Step 4: If the node is filled, we will follow the steps shown below.

Step 4.1: Insert the data elements in ascending order.

Step 4.2: Once the data elements exceed their limit, we will split the node at the median.

Step 4.3: We will then push the median key upwards, making the left keys the left child nodes and the right keys the right child nodes.

Step 5: If the node is not full, we will follow the below steps.

Step 5.1: We will insert the node in ascending order.

Let us understand the steps mentioned above with the illustrations shown below.

Suppose that the following are some data elements that need to be inserted in a B Tree: 7, 8, 9, 10, 11, 16, 21, and 18.

1. Since the maximum degree of a node in the tree is 3; therefore, the maximum number of keys per node will be 3 - 1 = 2.

2. We will start by inserting data element 7 in the empty tree.

Figure 2.1: Inserting 7

3. We will insert the next data element, i.e., 8, into the tree. Since 8 is greater than 7, it will be inserted to the right of 7 in the same node.

Figure 2.2: Inserting 8

4. Similarly, we will insert another data element, 9, into the tree on the same to the right of 8. However, since the maximum number of keys per node can only be 2, the node will split, pushing the median key 8 upward, making 7 the key of the left child node and 9 the key of the right child node.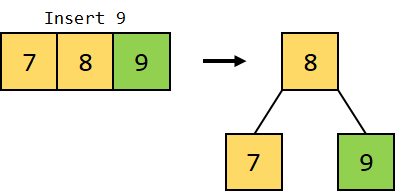

Figure 2.3: Inserting 9

5. We will insert the next data element, i.e., 10, into the tree. Since 10 is greater than 9, it will be inserted as a key on the right of the node containing 9 as a key.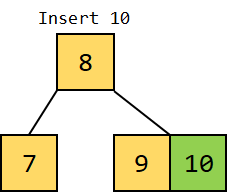

Figure 2.4: Inserting 10

6. We will now insert another data element, 11, into the tree. Since 11 is greater than 10, it should be inserted to the right of 10. However, as we know, the maximum number of keys per node cannot be more than 2; therefore, 10 being the median, will be pushed to the root node right to 8, splitting 9 and 11 into two separate nodes.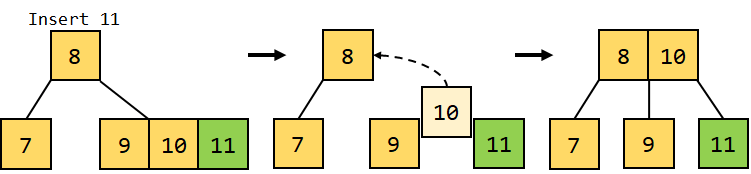

Figure 2.5: Inserting 11

7. We will now insert data element 16 into the tree. Since 16 is greater than 11, it will be inserted as a key on the right of the node consisting of 11 as a key.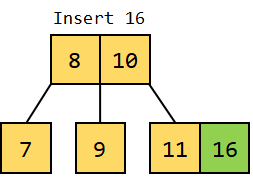

Figure 2.6: Inserting 16

8. The next data element that we will insert into the tree is 21. Element 21 should be inserted to the right of 16; however, it will exceed the maximum number of keys per node limit. Therefore, a split will occur, pushing the median key 16 upward and splitting the left and right keys into separate nodes. But this will again violate the maximum number of keys per node limit; therefore, a split will once again push the median key 10 upward a root node and make 8 and 11 its children.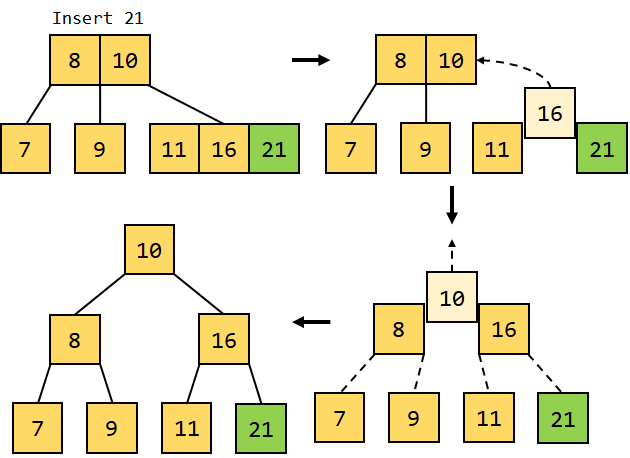

Figure 2.7: Inserting 21

9. At last, we will insert data element 18 into the tree. Since 18 is greater than 16 but less than 21, it will be inserted as the left key in the node consisting of 21.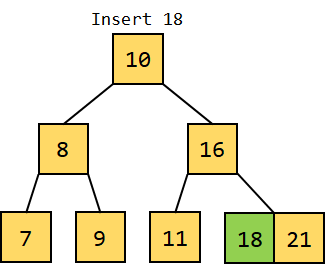

Figure 2.8: Inserting 18

10. Hence the resulted B Tree will be as shown below: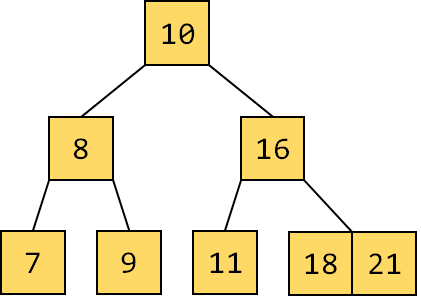

Figure 2.9: The Resulted B Tree

Algorithm for the Insertion of an element into a B Tree

We will now understand the algorithm we will use in order to insert a data element into a B Tree.

Pseudocode:

Let us now see the implementation of the above pseudocode in different programming languages.

Examples of Insertion Operation in B Tree

In the following section, we will see an implementation of the B Tree Insertion Operation based on the above algorithm in different programming languages such C, C++, Java, and Python.

Program to Insert Elements in a B Tree in C Language

Let us now consider the following program code illustrating how to insert data elements in a B Tree in C Language.

Program Code:

Output:

The B Tree is : 1 2 3 4 6 8 9 10 11 12 13

Explanation:

In the above snippet of code, we have included stdio.h and stdlib.h header files and defined some macros such as MAX and MIN. We have then defined the structure of the node of the B Tree using the struct keyword and created the node. We have then defined different functions to insert the value in the node, split the node, set the value of the node, insert elements in the B Tree, copy the successor, perform the right shift and left shift, merge the nodes, adjust the node, and traverse the tree. We have then defined the main function to execute the program where we have inserted different elements to the tree by calling the insertion_operation() function. At last, we have called the tree_traversal() function to print the elements of the node.

Program to Insert Elements in a B Tree in C++ Language

Let us now consider the following program code illustrating how to insert data elements in a B Tree in C++ Language.

Program Code:

Output:

The B Tree is : 1 2 3 4 6 8 9 10 11 12 13

Explanation:

In the above code snippet, we included the iostream header file and used the standard namespace. We have then defined a class to create the structure of the node of the B Tree. We have then defined another class to create the B Tree. We then created the node and defined different functions to traverse the tree, insert keys in it, non-full condition, and split the child node. At last, we have defined the main function and inserted different keys to the B Tree by calling the insertValue() function and called the tree_traversal() function to print the resultant tree.

Program to Insert Elements in a B Tree in Java Language

Let us now consider the following program code illustrating how to insert data elements in a B Tree in Java Language.

Program Code:

Output:

The B Tree is : 1 2 3 4 6 8 9 10 11 12 13

Explanation:

In the above snippet of code, we have defined the public class to create the B Tree. Within this class, we have defined another class to create the structure of the node. We have then created the B Tree and defined different functions to split the node, insert a key in the node, and display the Tree. We have defined the main function where we have called the insertValue() function to insert the key in the nodes. At last, we have also called the displayTree() function to display the resultant B Tree.

Program to Insert Elements in a B Tree in Python Language

Let us now consider the following program code illustrating how to insert data elements in a B Tree in Python Language.

Program Code:

Output:

The B Tree is : 1 2 3 4 6 8 9 10 11 12 13

Explanation:

In the above snippet of code, we have defined a class to create the structure of the node of the B Tree. Inside this class, we have declared necessary variables and defined some functions like a function to insert a new key in the subtree rooted with that particular node, split the child node, and traverse the tree. We have then defined another class to create the B Tree. Within this class, we have initialized some variables and defined different functions, like traversing the tree and inserting the value in the node. At last, we have defined the main function where we have inserted different keys to the tree using the insertValue() function and printed the resultant tree by calling the tree_traversal() function.

The Time Complexity of Insertion Operation in B Tree depends upon the number of nodes, and thus, is O(log n).

The Conclusion

In this tutorial, we have learned about the fundamentals of Insertion Operation in B Tree. We have also discussed the algorithm to carry the insertion of a key in the B Tree along with its implementation in different programming languages like C, C++, Java, and Python.