Angle Modulation

Angle modulation is the combination of frequency and phase modulation. We can also say that the frequency and phase combine to form an angle. Angle modulation is defined as the modulation where the frequency or phase of the carrier varies with the amplitude of the message signal. When the amplitude of the carrier varies with the message signal, it is known as amplitude modulation.

The spectral components of the modulated signal depend on the frequency and amplitude of the components in the baseband signal. Angle modulation is non-linear, while amplitude modulation is a linear process. The superposition principle does not apply in angle modulation.

The signal has the form of

V(t) = A cos [ω_ct + ϕ (t)]

Where,

ω_c is the carrier frequency constant

A is the amplitude constant

ϕ (t) is the phase angle, which is not constant. It is a function of the baseband signal.

Types of Angle Modulation

Angle modulation is the combination of phase and frequency modulation. It is the modulation where both the frequency and phase of the carrier vary with the amplitude of the message signal, as discussed above.

Angle Modulation is categorized as frequency modulation and phase modulation.

Frequency Modulation

If the frequency of the carrier varies with the amplitude of the message signal, it is known as frequency modulation. The amplitude of the modulated signal depends on the frequency difference between the carrier frequency and the center frequency. FM is a type of both analog and digital modulation. The applications of analog frequency modulation are telecommunications, computing, radio broadcasting, video broadcasting, and two-way radio systems. In digital modulation, the process used to transmit digital data using FM is known as Frequency-Shift Keying.

Phase Modulation

If the carrier phase varies with the amplitude of the message signal, it is known as phase modulation. In angle modulation, it is together used with frequency modulation. It is also an integral part of both analog and digital communication. In analog communication, phase modulation is used for transmitting radio waves and other technologies, such as Wi-Fi and satellite television.

The waveforms of frequency modulation and phase modulation are shown below: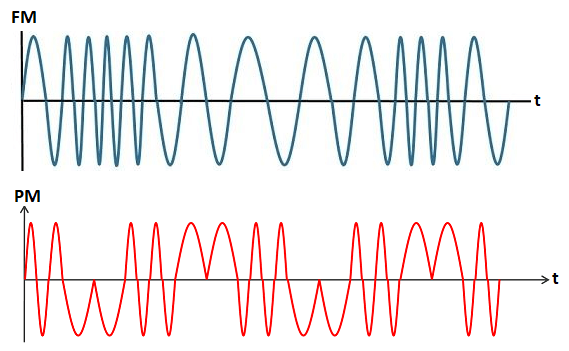

Relationship between Frequency and Phase Modulation

The block diagram of frequency modulation consists of an integrator and a phase modulator, as shown below: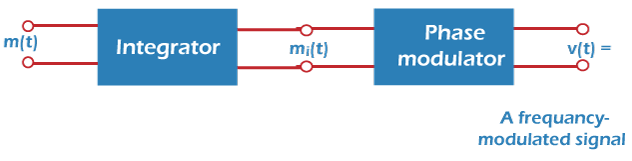

The modulating signal is applied to the integrator, which is further sent to the phase modulator. The output of the combination of the integrator and the phase modulator is the frequency modulated signal.

Let the message signal and the frequency constant be m(t) and K_F.

Where,

K_F =KK_P

The output of the phase modulator is given by: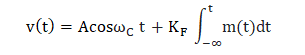

The block diagram of the phase modulation consists of a differentiator and a frequency modulator, as shown below: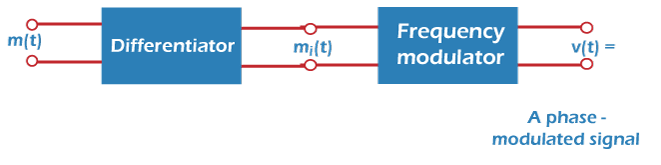

The modulating signal is applied to the differentiator, which is further sent to the frequency modulator. The output of the combination of the differentiator and frequency modulator is the phase modulated signal.

Let the phase constant be K_P.

The output can be represented as:

V(t) = A cos [ω_ct + K_P m(t)]

Where,

ω_c is the carrier frequency constant

A is the amplitude constant

m(t) is the instantaneous value of the message signal

The instantaneous angular frequency is the differentiation of the output of the frequency modulator. It is given by: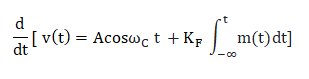

ω = ω_c + K m(t)

The maximum frequency component of the message signal and instantaneous value of the message signal is F_M. The integral part of the frequency modulation is a linear operation and does not change the number of frequency components.

Modulation Index

The deviation of the total angle from the carrier angle is defined as phase deviation. The deviation of the total angle from the carrier angle is defined as phase deviation. The instantaneous frequency deviation from the carrier frequency is known as frequency deviation.

The frequency of the message signal is represented as ω_m

ω_m = 2πF_m

The angle modulated signal is given by:

V(t) = A cos [ω_ct + Bsin ω_mt] … (1)

Where,

ω_c is the carrier frequency constant

A is the amplitude constant

ω_c is the message frequency constant

B is the peak amplitude of the phase constant ϕ (t)

The instantaneous frequency is represented as ω.

ω = d/dt [ϕ]

ω = d/dt [[ω_ct + Bcosω_mt]

ω = ω_c + Bω_m cos ω_mt

We know,

ω = 2πF

Substituting the value of ω = 2πF, we get:

2πF = ω_c + Bω_m sin ω_mt

F = ω_c/2π + Bω_m sin ω_mt /2π

F = F_C + BF_m sin ω_mt

Where,

F_C = ω_c/2π

F_m = ω_m/2π

The maximum frequency deviation is represented as Δf.

Δf = BF_m

Thus, equation (1) can be represented as:
V(t) = A cos [ω_ct + Δf / F_m sin ω_mt]

In the next section, we will discuss FM (Frequency Modulation) and Phase Modulation (PM) in detail.

Numerical Examples

Let's discuss some numerical examples based on the angle modulation.

Example 1: Consider an angle modulated signal P(t) = 5cos [2π 10⁶t + 3sin (2π 10⁴t)]. Find its instantaneous value at t = 0.8 ms?

Solution:

Given: Phase ϕ (t)= 2π 10⁶t + 3sin (2π 10⁴t)

Instantaneous frequency = dϕ (t)/dt

= d/dt [2π 10⁶t + 3sin (2π 10⁴t)]

= 2π 10⁶ + 2π 10⁴ 3cos (2π 10⁴t)

At, t = 0.8ms

t = 0.8 x 10^-3 seconds

Substituting the value of t, we get:

= 2π 10⁶ + 2π 10⁴ 3cos (2π 10⁴ × 0.8 x 10^-3)

= 2π 10⁶ + 2π 10⁴ 3cos (16 π)

= 2π 10⁶ + 2π 10⁴ 3 (1)

(cos16 π = 1)

= 2π 10⁶ + 6π 10⁴

= 2π 10⁴ (10² + 3)

= 2π 10⁴ (103)

= 6.47 ×10⁶ Hz

= 6.47M Hz

Thus, the instantaneous value is 6.47M Hz.

Example 2: Consider an angle modulated signal P(t) = 3cos [2π 10⁸t + 5sin (2π 10⁵t)]. Find its instantaneous value at t = 0.5 ms?

Solution: Given: Phase ϕ (t)= 2π 10⁸t + 5sin (2π 10⁵t)

Instantaneous frequency = dϕ (t)/dt

= d/dt [2π 10⁸t + 5sin (2π 10⁵t)]

= 2π 10⁸ + 2π 10⁵ 5cos (2π 10⁵t)

At, t = 0.5ms

t = 0.5 x 10^-3 seconds

Substituting the value of t, we get:

= 2π 10⁸ + 2π 10⁵ 5cos (2π 10⁴ × 0.5 x 10^-3)

= 2π 10⁸ + 2π 10⁵ 5cos (10 π)

= 2π 10⁸ + 2π 10⁵ 5 (1)

(cos 10 π = 1)

= 2π 10⁸ + 10π 10⁵

= 2π 10⁵ (10³ + 5)

= 2π 10⁴ (1005)

= 6.314 ×10⁸ Hz

Thus, the instantaneous value is 6.314 ×10⁸ Hz.