Digital Signal Processing MCQ1) The product of two odd signals is:
Answer: (b) Even Description: Let x1(n) and x2(n) be the two signals. If both these signals are odd, x1(-n) = - x1(n) and x2(-n) = - x2(n) If a signal is even, x(-n) = x(n) x(-n) = x1(-n) . x2(-n) x(-n) = - x1(n). - x2(n) x(-n) = x1(n). x2(n) It means that x(-n) = x(n), which is even. Hence, the product of two odd signals is even. 2) The system given by y(n) = x(n) + 1/x(n - 1) is:
Answer: (b) Causal Description: Step 1: The system is causal if its output depends only on the past and present inputs. Let's check its causality. We will check the value of y(n) for different values of n. For, n= 0, y(0) = x(0) + 1/x(-1) n = 1, y(1) = x(1) + 1/x(0) Thus, the system is causal. Step 2: The system that satisfies the superposition theorem can be classified as the linear system. Y1(n) = x1(n) + 1/x1(n - 1) Y2(n) = x2(n) + 1/x2(n - 1) To satisfy the linearity, ay1(n) + by2(n) = ax1(n) + bx2(n) LHS ay1(n) + by2(n) = a [x1(n) + 1/x1(n - 1)] + b [x2(n) + 1/x2(n - 1)] ay1(n) + by2(n) = ax1(n) + bx2(n) + a/x1(n - 1) + b/x2(n - 1) It is not equal to RHS Hence, the system is non-linear. 3) Which of the following is not a type of discrete system?
Answer: (d) Non-dynamic systems Description: The system can be classified as static, dynamic, causal, non-causal, recursive, non-recursive, etc. Non-dynamic is not a type of discrete system. 4) The advantages of discrete signal processing is/are:
Answer: (d) All of the above Description: The advantages of the DSP are low cost, time sharing capability, and high flexibility. 5) Which of the following is the characteristic of the power signal?
Answer: (a) Power signal is infinite. Description: The power signal is infinite because it exists over an infinite duration. Hence, it is not time-limited. Periodic signals are the power signals, while Aperiodic is the energy signals. 6) The Digital Signal Processing system:
Answer: (d) Both (a) and (c) Description: Analog-Digital Processing is not applicable for low-frequency signals. Digital Signal Processing consumes more power and applicable for low-frequency signals. 7) The length of the output sequence (n) of the two sequences (n1 and n2) can be calculated using the formula:
Answer: (b) n = n1 + n2 - 1 Description: The formula to calculate the length of the sequence of two signals is n = n1 + n2 - 1. For example, If, n1 = 4 and n2 = 3, n = 4 + 3 - 1 = 6 8) An analog signal has a bandwidth of 5KHz. If we are using an N-point DFT to compute the signal spectrum with a resolution less than or equal to 25Hz. Find the minimum length of the signal.
Answer: (b) 0.04s Description: Given, Bandwidth = 5 KHz. N = 2^m, where m is the integer Minimum length of the signal (T) is given by: T = L/Fs Where, L is the minimum number of requires samples Fs is the minimum sampling rate Fs = 2fm It means that the sampling rate is twice the bandwidth. Fs = 2 x 5 = 10 KHz. L = Fs/Resolution So, T = (Fs/ Resolution)/ Fs T = 1/Fs T = 1/25Hz T = 0.04s 9) One-sided Z-transform is also known as:
Answer: (a) Unilateral Z-transform Description: Two-sided Z-transform is known as bilateral transform. One-sided is known as Unilateral Z-transform. 10) The Z-transform of the function y(n) = x(n) + y(n - 1) is:
Answer: (c) z/ z - 1 Description: Given signal: y(n) = x(n) + y(n - 1) Applying Z-transform on both the sides, Z [y(n)] = Z [x(n)] + Z y[(n - 1)] Y(z) = X(z) + z^(-1) Y(z) Y(z) - z^(-1) Y(z) = X(z) Y(z) (1 - 1/z) = X(z) Y(z) (1 - 1/z) = X(z) Y(z)/X(z) = 1/ (1 - 1/z) H(z) = z / z-1 Thus, the Z-transform of the function y(n) = x(n) + y(n - 1) is z / z-1, which is option (c). 11) The z-transform of the signal a^nx(n) is:
Answer: (b) X(z/a) Description: The above property is defined as the scaling property of the signal. The z-transform of the signal a^nx(n) is X(z/a). 12) The z-transform of the impulse response y(n) = x(n) + 2x(n - 1) is:
Answer: (a) 1 + 2z^- 1 Description: The Z-transform of a sequence n is given by: 
Z [y(n)] = Z [x(n)] + Z [2x(n - 1)] Y(z) = X(z) + 2z^-1X(z) Y(z) = X(z) (1 + 2z^-1) Y(z)/X(z) = 1 + 2z^-1 H(z) = 1 + 2z^-1 13) The addition of zeroes at the end of the sequence when it is represented as the power of integer is refer as:
Answer: (c) Zero padding Description: Zero padding is generally used in circular convolution if the lengths of the two given sequences are not equal. 14) The z-transform of the system h(n) = 3^n u(n) is:
Answer: (d) z/ z - 3 Description: Z-transform is given by: 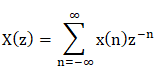
So, 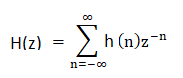
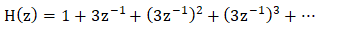
H(z) = 1/(1 - 3/z) H(z) = z/ z - 3 Hence, z-transform of the system h(n) = 3^n u(n) is z/ z - 3. 15) The system that accepts the input in the discrete form and produces the discrete time output is known as:
Answer: (b) Discrete time system Description: The discrete time system accepts the input and produces the output in the discrete form. 16) Find the number of smallest DFTs required to compute the linear convolution of length 40 sequences with a length of 900 another sequences using 64 DFT.
Answer: (a) 36 Description: Let the two sequences be M and N. M = 40 N = 900 Number of DFT = 64 The number of smaller DTS required = L + M - 1 = Number of given DFT points L + M - 1 = 64 L + 40 - 1 = 64 L = 25 Total blocks = N / L = 900/25 = 36 Hence, the number of smallest DFTs required to compute the linear convolution is 36. 17) Determine the number of complex additions required for 32 direct computations of DFT.
Answer: (c) 992 Description: The number of complex additions is given by N (N - 1). Where, N is the number of direct DFT computations Here, N is 32. So, complex additions = 32 (32 - 1) = 32 x 31 = 992 18) Find the complex multiplications required for 16 direct computations of DFT.
Answer: (a) 256 Description: The complex multiplications are given by N^2. Where, N is the number of direct DFT computations Here, N is 16. So, complex multiplications = 16 x 16 = 256. 19) Which of the following statement is incorrect about DIT- FFT?
Answer: (d) The output sequence is represented in bit-reversal order. Description: The output sequence of the DIT-FFT is represented in regular order instead of bit-reversal order. 20) Which of the following statement is/are correct about linear convolution? 1. The Input and output sequence is Aperiodic. 2. It requires zero padding. 3. The length of the input and output sequence is the same. 4. The length of output sequence is greater than the input sequence.
Answer: (c) 1 and 4 Description: The linear convolution does not require the use of zero padding. The length of output sequence is greater than the input sequence length. 21) IDFT of the sequence {1, 0, 1, 0} is:
Answer: (b) {0.5, 0, 0.5, 0} Description: IDFT is given by: x(n) = IDFT [X(k)] 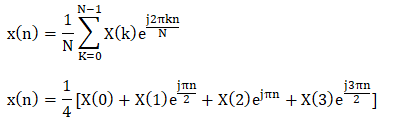
Step 1: For, n = 0 x(0) = ¼ [ x(0) + x(1) + x(2) + x(3)] = ¼[1 + 0 + 1 + 0] = 2/4 = 1/2 = 0.5 Step 2: For, n = 1 x(1) = ¼ [ x(0) + x(1) + x(2) + x(3)] = ¼[1 + 0(j)+ 1(-1) + 0(-j)] = ¼ [1 +0 -1 + 0] = 0 Step 3: For, n = 2 x(2) = ¼ [ x(0) + x(1) + x(2) + x(3)] = ¼[1 + 0(-1)+ 1(1) + 0(-1)] = ¼[1 + 0 + 1 + 0] = 2/4 = 1/2 = 0.5 Step 4: For, n = 3 x(3) = ¼ [ x(0) + x(1) + x(2) + x(3)] = ¼[1 + 0(-j)+ 1(-1) + 0(j)] = ¼ [1 +0 - 1 + 0] = 0 Thus, x(n) = {0.5, 0, 0.5, 0} 22) The algorithm used for the computation of DFT based on the decomposition of N-point DFT is known as:
Answer: (c) Divide and conquer. Description: Divide and conquer in the approach that is considered as an efficient algorithm for the computation of DFT based on the decomposition of N-point DFT. 23) The formula to calculate the complex additions in the case of the divide and conquer approach is:
Answer: (d) N (M + L - 2) Description: The complex additions are given by N (M + L -2). Where, M and L are the integers of the given data array, and N is the number point DFT. The number of complex additions for the above approach is less than the direct form approach. 24) Determine the number of complex multiplications for the 8-point Radix-2 FET.
Answer: (b) 12 Description: The number of complex multiplications is given by: N/2(log2N) Where, N is the point DFT. Thus, the complex multiplications = 8/2 (log2 8) = 4 x 3 = 12. 25) The advantages of the butterfly structure is:
Answer: (d) All of the above Description: Butterfly structure is an efficient structure that has various advantages, such as reducing complexity, involvement of less number of multiplications and additions. It also combines the result of small DFTs into large or vice versa. 26) Which of the following is/are incorrect about the Cascade realization of the IIR systems?
Answer: (c) The filters in the cascade are connected in parallel. Description: The filters in the cascade realization are connected in series. 27) Linear phase response of the filter is defined as:
Answer: (a) When the phase response of the system varies linearly with the frequency function. Description: As the name specifies, the phase response of the system varies linearly with the frequency. 28) Which of the following statement is/are incorrect about the FIR filters? 1. FIR filters are always stable. 2. It requires more memory as compared to IIR filters. 3. FIR filters are non-canonical. 4. Its linear phase realization structure can be easily designed.
Answer: (c) Only 3 Description: FIR filters are generally canonic filters. The non-canonical filters are the IIR filters. 29) Digital filters are:
Answer: (c) Programmable. Description: Digital filters are programmable, less expensive, and consume high power. It can easily handle low-frequency signals. The operation of the digital filter is determined by a program, which is stored in the memory of the processor. Hence, these filters are generally programmable. 30) The method responsible for introducing the aliasing effect in filters is:
Answer: (a) Impulse invariant method Description: The practical analog filters are not generally perfectly band-limited. Hence, the filter using the impulsive invariant method can cause such an aliasing effect in the filters. 31) Which of the following is/are features of the digital signal processor?
Answer: (d) Both (a) and (b). Description: On-chip registers of the processor can store intermediate results. Thus, option (c) is incorrect. 32) Determine the discrete equation of the direct form-I structure shown in the below figure: 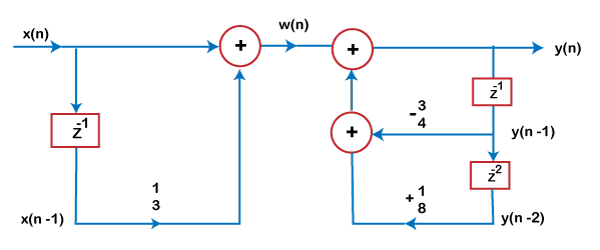
Answer: (b) 3/4 y(n - 1) - 1/8 y(n - 2) + x(n) + 1/3x(n - 1) Description: The direct form-I is the structure formed after finding the z-transform of X(z) and Y(z), which is mentioned on both sides of the figure. Let's first determine X(z) and Y(z) and then their inverse Z-transform to find the equation of the discrete system. Step 1: LHS The left side is the X(z). X(z) [1 + 1/3 z^-1] = W(z) X(Z) + 1/3 z^-1 X(z) = W(z) The inverse can be represented as: x(n) + 1/3x(n - 1) = w(n) Step 2: RHS The right side is the Y(z). Y(z) = 3/4 z^-1 Y(z) - 1/8 z^-2 Y(z) + W(z) The inverse can be represented as: y(n) = 3/4 y(n - 1) - 1/8 y(n - 2) + w(n) Substituting the value of w(n) from step 1, we get: y(n) = 3/4 y(n - 1) - 1/8 y(n - 2) + x(n) + 1/3x(n - 1) It is the discrete equation of the given system. 33) Which of the following bus is used in the Digital signal processor?
Answer: (d) Both (a) and (b) Description: The two buses program memory bus and data memory bus provides an additional interface to the processor. 34) Which of the following form is used for the IIR filters?
Answer: (a) Direct form- I Description: There are two types of direct form, direct form I and direct form-II. Both forms can be used for IIR (Infinite Impulse Response) filters. 35) The structure of the direct form- II is shown in the below figure. Determine the order of the system? 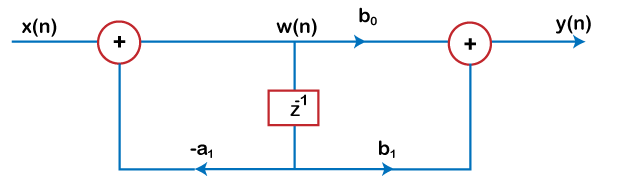
Answer: (b) First order system. Description: The above figure displays only one value of z^-1, which specifies that the system is of the first order. 36) The multipliers required for the (M - 1) and (N - 1) order IIR filters are given by:
Answer: (c) M + N - 1 Description: The multipliers of IIR filters are given by: M + N - 1 37) Find the number of block of the processed data with the input samples 16000 and the filter length 100. Assume the block size of FFT be 1024.
Answer: (a) 17 Description: Given, N = 1024 M = 100 L = N - M + 1 = 1024 - 100 + 1 = 925 No. of blocks of the processed data = Input samples/ 925 = 16000/925 = 17.29 = 17 38) The incorrect statement about FIR filters is?
Answer: (d) FIR filters are not immune to noise. Description: FIR filters are highly immune to noise. 39) Which of the following feature about the triangular window technique used in the FIR filter design is correct?
Answer: (d) Its side lobe magnitude of the window spectrum remains constant. Description: The main lobe width is twice that of rectangular window. The minimum stop band attenuation required is around 31 dB. 40) The incorrect statement about the effects of windowing in filters is:
Answer: (d) None of the above Description: All the statements about the windowing technique are correct. 41) The window technique whose main lobe width is 12pi/N is called:
Answer: (b) Blackmann window Description: The main lobe width of the Blackmann window is greater than all other window techniques, which is equal to 12pi/N. 42) Which type of filters are all pole filters?
Answer: (a) Type- I Chebyshev filters Description: Type- II Chebyshev filters contain poles as well and zeros. Hence, Type- I Chebyshev filters are all pole filters. 43) Which of the following statement is correct about Butterworth filters? 1. The magnitude response of the Butterworth filter has ripples in the pass-band. 2. Its pole lies on a circle in the s-plane. 3. Its design requires fewer parameters. 4. Its pole lies on an ellipse in the s-plane.
Answer: (b) 2 and 3 Description: The poles of the Butterworth filter lies on a circle, not on an ellipse. The magnitude response of the Chebyshev filters has ripples in the pass-band instead of the Butterworth filter. 44) The incorrect statement about the Impulse Invariant method is:
Answer: (c) Absence of many-to-one mapping. Description: The presence of many-to-one mapping is a primary drawback of the impulse invariant method. It means that many points in the s-plane are mapped to a single point in the z-plane. It can also cause an aliasing effect in the filters. 45) The Nyquist sampling rate is given by:
Answer: (a) Fs = 2 Fm Description: The Nyquist sampling rate is twice the maximum frequency. 46) Which of the following is/are standard test signals?
Answer: (d) All of the above Description: The standard test signals are categorized as step, impulse, exponential, ramp, sinusoidal, etc. Hence, all three options are correct.
Next TopicIndian Constitution MCQ
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share










