Engineering Mechanics MCQsOur top 50 Engineering Mechanics questions and answers focus on all the areas of this subject. It covers over more than 50 topics in Engineering Mechanics. Anyone who wishes to sharpen their knowledge, preparing for the interviews, or preparing for the entrance exam can practice these Engineering Mechanics Questions. 1) For two vectors defined by an arrow with a head and a tail. The length of each vector and the angle between them represents:
Answer: A [ Their magnitude and direction of the line of action, respectively ] Description: The length of each vector and the angle between them represent their magnitude and direction of the action line, respectively. The head/tip of the arrow indicates the sense of direction of the vector. 2) A force vector with magnitude R and making an angle α with the x-axis is having its component along the x-axis and y-axis as:
Answer: B [ Rcosine (α) and Rsine(α) ] Description: The component along the x-axis is the cosine component of the vector. And the y-axis component of the vector is the sine component if the angle is being made with the x-axis. And 180- α for some of the trigonometric functions may change their sign. 3) Shown as in the figure below, A=60 degree and B=30 degree. Calculate the total length obtained by adding the x-axis component of both vectors. 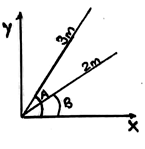
Answer: B [ 3.23m ] Description: After getting the cosine components of the given vectors, we obtain the total length of the x-axis components to be 3cos60 + 2cos30 = 3.23. 4) If two equal vector forces are mutually perpendicular, then the resultant force is acting at which angle as compared to one of the vector?
Answer: B [ 45 degrees] Description: The vectors are mutually perpendicular. It means that the angle between the forces is 90 degree. Thus the results will form at 45 degrees to any of the vector. 5) If A is any vector with Ai + Bj + Ck, then what is the y-axis component of the vector?
Answer: B [ B units ] Description: As the given vector is shown in the Cartesian system, the number with "j" is the given vector's Y-axis component. The numbers with "i" represent components of the x-axis and "k" representing the z-axis, respectively. 6) Which statement is right for force vector F = Ai + Bj + Ck?
Answer: In rectangular components representation of any vector we have vector F = Fx + Fy + Fz Description: As given the vector is F = Ai + Bj + Ck, this implies that the x,y, and z-axis components of this vector are A, B, and C, respectively. But, in the rectangular component's representation of any vector, the vector is written as F = Fx + Fy + Fz. 7) For a vector F, Fcosβ is equal to zero. What does this refer to?
Answer: A [ Y-axis component is zero ] Description: As we know, the α, β, and γ are the angles made by the x, y, and z-axis, respectively. Thus y-axis component is zero, or β = 90°. Thus, if the angle gives a component to zero, the vector in that particular axis is perpendicular to that axis. 8) Find the angle α, for the vector making an angle by y and z-axis as 60° and 45°, respectively. It makes an angle of α with the x-axis. The magnitude of the force is 200N.
Answer: B [ 60° ] Description: When you will resolve the vector in its x, y, and z-axis components, you will get an equation containing cosα. After getting the α correctly, you need to put that value in the previous equation of components directly. α = 60°. As 120° will give a negative component. Just try to resolve the vector in its components. 9) Express the vector in the Cartesian Form if the angle made by it with y and z-axis is 60° and 45° respectively. Also, it makes an angle of α with the x-axis. The magnitude of the force is 200N.
Answer: B [ 100i + 100j + 141.4k N ] Description: When you will resolve the vector in its x, y, and z-axis components, you will get an equation containing cosα. After getting the correct, you need to put that value in the previous equation of components directly. 10) What if we multiply a scalar to the unit vector?
Answer: A [ The magnitude will change accordingly ] Description: The magnitude of the unit vector will change by the amount of the scalar multiplied. Not the direction. Because the direction is being fixed after applying the unit vector's calculation, the vector is divided by its magnitude. 11) Which statement is right?
Answer: B [ Communitive law: A.B =B.A ] Description: For three vectors A, B and D the various laws are. Communitive law: A.B =B.A. While distributive law is A.(B+D) = (A.B) + (A.D). And multiplication law is a(A.B) = A.(aB). 12) What is (AxB).(BxA); or A = A1i + A2j + A3k and B = B1i + B2j + B3k?
Answer: D [ 0 ] Description: Here, we are trying to do the two vectors' cross product in the same plane, which will give us zero. Simultaneously, the dot product of the same plane vector will give a scalar quantity, not zero. 13) What is the dot product of two vectors which are having a magnitude equal to unity and are making an angle of 45°?
Answer: B [ 0.707 ] Description: The dot product of two vectors having the angle between them equal to 45° will have the product of the vector's magnitude. As the vectors are of unit magnitude, their product will be unity. Thus the magnitude factor would be cosine function at 45 °. 14) What is the magnitude of the resultant vector's unit vector? (Resultant vector of the two vectors shown in the figure below) 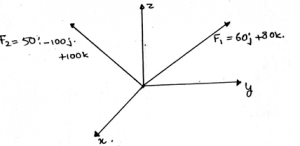
Answer: B [ 1N ] Description: The question asked is asking for the magnitude of the unit vector of the resultant vector. Thus the answer is 1. Whether the vector's magnitude is any quantity, the unit vector will have a magnitude equal to unity. And the direction given by the unit vector will be in the same direction as that of the vector. 15) Determine the value of the q, parallel to the z-axis. That is the point of intersection of the projections of the points A, B, and C parallel to the xy plane. The distance between the tri-section point and the points A, B, and C be equal to 0.6m. 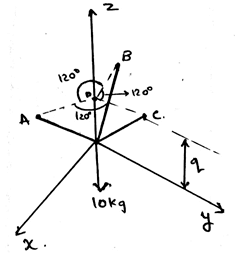
Answer: B [ 51.9cm ] Description: The application of the equilibrium equation will yield the result. The resultant along the z-axis will remain zero, which gives the value of γ as 50°. And therefore q=51.9cm. 16) If anybody is tied to three or more ropes and is allowed to achieve its equilibrium. Then the equilibrium achieved is achieved w.r.t what?
Answer: A [ The ground ] Description: Yes, the equilibrium is being achieved w.r.t the ground. Like the motion, w.r.t ground need be zero. The relative velocity of the object or the body must be zero w.r.t the ground. This means motion is in equilibrium. 17) The tendency of rotation of the body along any axis is also called ______
Answer: D [ Torque ] Description: The tendency of rotation of the body along any axis, also called the torque. It is the moment of the force acting perpendicular to the direction of the axis of rotation. If the axis and the force are meeting, then there is no moment applied by force. 18) The moment is the cross product of which two vectors?
Answer: A [ Radius and Force vectors ] Description: The cross product needs to take in the proper sequence. If not taken, then the answer is just the opposite of the true answer. That's why the answer is not the Force and Radius vectors but the Radius and Force vectors. Because the moment has its direction, as many of the cross products have, precaution needs to be taken. 19) Which of the following is correct w.r.t the moment (M) of the force (F) acting on the body at a distance L from the axis of the rotation?
Answer: B [ M=FLsinθ ] Description: The moment of the force about the axis of rotation by the application of the force on the body is given by the cross product of both. If the force was not perpendicular to the axis and angle θ, the form of angle is used. As usually used in the cross product. 20) If a force is applied at any point in its line of action and is still creating the same moment about any fixed point, say P, then the force is said to be a sliding vector. What is the name of this property?
Answer: C [ Principle transmissibility of the force ] Description: If a force is applied at any point in its line of action and is still creating the same moment about any fixed point, say P, then the force is said to be a sliding vector. This is because the moment of the force which is acting on its line of the axis at point P is the same throughout. It is known as the principle transmissibility of the force. 21) Which of the following is correct? (For A representing the vector representation of the axis of rotation, r the radius vector and F the force vector)
Answer: A.(rxF) Description: The correct form of the equation is given by A.(rxF). A represents the vector of the rotation's axis, r the radius vector, and F the force vector. Usually, it can be done to determine the moment of the force about the axis. That is if the force is rotating the body about an axis. 22) Which of the following forces do not cause the rotation. Suppose the rotation is considered inside the body's axis or the centroid axis of the body.
Answer: A [ Concurrent ] Description: The concurrent forces are the axis of rotation. If any of the force touches that axis, that force is not considered insufficient to cause a rotation. If a force is concurrent, then the force's perpendicular distance from the axis line is zero, thus no rotation. As we know, rotation is caused by a moment. 23) Which of the following is correct for the moment of couple M caused by two forces of the same magnitude F and are separated by a distance of r?
Answer: B [ M = rxF ] Description: The answer is M = rxF. The moment is the cross product of the distance and the forces. It is the direction as directed by the curling of the hand. The thumb is representing the direction of the moment. The finger's motion is the rotation that gives the direction of the rotation caused by the forces. 24) Determine the couple moment acting on the triangular plane shown. 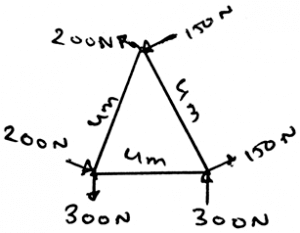
Answer: 2600Nm 25) The principle of transmissibility is
Answer: B [ It states that the force acting on the body is a sliding vector ] Description: The principle of transmissibility states that the force acting on the body is a sliding vector. That is, it can be applied at any point of the body. It will give the same effect as if applied at any point other than the specific point. Thus the answer. 26) What is the main motto of simplification?
Answer: B [ To reduce the calculation ] Description: The main moto of simplification is to reduce the calculation. The forces are simplified, and the couples to are simplified. This gives us the total force and the total moment acting on the body. This gives us a single value of the respective thing and hence reduces the work. 27) Just like the collinear forces, there is a collinear couple, and the net moment is taken out from it.
Answer: D [ The first part of the statement is true, and the other part is false ] Description: Both of them are vector quantities. And both of them can be easily simplified. If taken in the vector form, then the task is even easier. Thus it is not necessary for the force or the couple to be vector only. Even if the magnitude is taken, the simplification is done in the 2D. 28) There are two types of loading. The uniformly distributed and the non-uniformly distributed, that is the one having two different values at corners.
Answer: C [ The first part of the statement is true, and the other part is true too ] Description: The two loading forms are uniformly distributed and non-uniformly distributed with two different values at corners. The uniform distributed load is not having two different values of the load per unit meter on the corner. 29) In the simplification of the loading system, the net force acts at the ___________ of the loading body.
Answer: B [ Centroid ] Description: In simplifying the loading system, the net force acts at the loading body's centroid. If the loading system is in the form of the triangle, then at a distance two by 3 of the base, the loading's net force will act. And the load will be half the area of the loading. 30) In triangle distributed loading, the loading at any distance can be easily found by using which of the following trigonometry function?
Answer: B [ Tangent ] Description: In triangle distributed loading, the loading at any distance can be easily found by using the Tangent trigonometry function. That is because the linear distance only determines the vertical loading. That is, the loading is uniform along with the linear distance. If the linear distance is more, the loading is more. 31) The resultant force acting of the uniformly distributed loading is dependent on:
Answer: B [ Area ] Description: The resultant force acting of the uniformly distributed loading is dependent on the area that the distribution is covering. The more the area, the more is the force. That is more the tension created over the structure on which loading is kept. Hence the answer. 32) Determine the vertical components of the reaction on the beam caused by the pin at Q. The force 60N is multiplied by ten and then is applied. 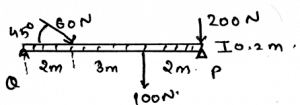
Answer: B [ 319N ] Description: The summation of the forces needs to be zero. So does the summation of the moments need to zero? But talking about the angles, they not needed to zero. But the forces acting at particular angles must be equal to zero?the basic need of the forces to put the body in equilibrium. 33) Which of the following statement for the three force system is true?
Answer: A [ The forces are always in equilibrium ] Description: The forces in the three-force system are not always in equilibrium. The equilibrium is established when the forces cancel out each other. Also, when the net moment is zero. Then only the equilibrium is established in the three force system. 34) A force is developed by the support that not allows the ________ of its attached member.
Answer: B [ Translation ] Description: The force developed by support doesn't allow the translation of its attached member. This is the basic condition for the equilibrium of the forces in any dimension. This rule is applied when the support reactions are taken into account for the body's equilibrium. 35) The single pin, single bearing, and single hinge resist _____
Answer: D [ Both force and couple moments ] Description: The experiments have founded that the single pin, single bearing, and single hinge resist both force and couple moments. It helps in attaining the equilibrium of the body. Thus proper guidance must be taken while solving the question on the same. 36) If the supports are properly aligned, the reaction forces developed adequately support the body.
Answer: D [ Statement is true throughout ] Description: This is the basic nature observed during the experiments on the beams and all the support systems. The dimension doesn't affect the equilibrium conditions. The main motto is to achieve equilibrium. It is achieved by equating the net force equal to zero. 37) What is redundant support?
Answer: C [ The supports more than necessary to hold the structure ] Description: The supports, if they are more than the supports required to hold the structure, are termed as the reductant supports. It becomes statically indeterminate. It creates a problem in achieving the equilibrium and affects the calculation of the equilibrium. 38) What is Statically indeterminacy?
Answer: B [ There will be fewer equations available for equilibrium than the unknown loadings ] Description: Statically indeterminacy is the condition when fewer equations are available for equilibrium than the unknown loadings. It not only creates a problem in achieving the equilibrium but also affects the calculation of the equilibrium. Thus this is the stuff that one needs to prevent from happening. 39) In 3D, the body will be improperly constrained if the reaction forces intersect the axis.
Answer: B [ The statement is right ] Description: In 3D, the body will be improperly constrained if the reaction forces intersect the axis. It is because there will be small moments that will occur in real situations. But they will not be matched in the calculations done for determining the equilibrium. Thus the statement is right. 40) The couple is a scalar quantity, and the force is a vector quantity; hence, only force can be simplified in free body diagrams.
Answer: B [ The first part of the statement is false, and the other part is true ] Description: Both of them are vector quantities. And both of them can be easily simplified. If taken in the vector form, then the task is even easier. Thus it is not necessary for the force or the couple to be vector only. Even if the magnitude is taken, the simplification is done in the 2D. 41) The couple and the other two force systems in free body diagrams can be easily simplified.
Answer: A [ Statement is right ] Description: Both of them are vector quantities. And both of them can be easily simplified. If taken in the vector form, then the task is even easier. Thus it is not necessary for the force or the couple to be vector only. Even if the magnitude is taken, the simplification is done in the 2D. 42) What is a collinear system of forces for free body diagrams?
Answer: D [ The force system having all the forces emerging from a single point ] Description: The force system having all the forces emerging from a point is called the force's collinear system. It is a type of system of force, which is easy the simplification. As the forces are the vector quantity, the vector math is applied, and the simplification is done. 43) To design the trusses, which of the following rules is followed?
Answer: A [ The loads are applied at the joints ] Description: The set of rules which are used to design the trusses have various rules. To them, one is that the loads are applied at the joints. It is done with the neglecting of the weight of the trusses section. 44) What does Newton's third law state?
Answer: A [ For every reaction, there is an equal and opposite reaction ] Description: The requirement of the third law is important in the equilibrium of the body. Especially the rigid bodies. The rigid body particles are in equilibrium. Due to which they are facing the forces. They also react and apply the opposite force, and thus Newton's third law to be in equilibrium. 45) If the body is in equilibrium, but it is having a rotational curled ray shown in the free body diagram, then:
Answer: C [ The body is said to be in equilibrium only, as the other forces will cancel out that rotation ] Description: The body having equilibrium will not rotate at any cost. Yes, the diagram may contain the rotational array showing the couple being acted over the structure. But the thing is that the forces, i.e., the other forces outside the dependency of this rotation, will cancel out this rotation, and thus the body is in equilibrium. 46) If five forces are acting on the single-particle and having an angle of 72° between each and are collinear, then:
Answer: B [ The net force acting on the body is zero ] Description: The net force acting on the body is zero. It means that the forces cancel out. This means that the body is in equilibrium and doesn't need any external force to make itself in equilibrium. 47) The difference between the two and the three force members is:
Answer: C [ The former is acting on two points in the body while the latter is on three points ] Description: The two force member's definition only defines that the forces are acting on the two points on the body. So does is the definition of the three forces members. The points of action of the three forces are three. 48) Which of the following statement for the three force system is true?
Answer: A [ The forces are not always in the equilibrium ] Description: The forces in the three-force system are not always in equilibrium. The equilibrium is established when the forces cancel out each other. Also, when the net moment is zero. Then only the equilibrium is established in the three force system. 49) All the forces need to be collinear in the three-force system. Then only will they for the equilibrium state.
Answer: C [ The first part of the statement is true, and the other part is true too ] Description: The forces need to be collinear. If they are not so, then the equilibrium is not possible. If they are parallel, too, then it is assumed that they are meeting in infinity. And hence the equilibrium is established between the forces. Thus the forces must be collinear. 50) A couple of moment is developed when _______ of the attached member is prevented.
Answer: A [ Rotation ] Description: The development of the couple moment is when there is a prevention of the attached member's rotation. This is the basic condition for the equilibrium of the couple moments in any dimension. This rule is applied when the couple moments are taken into account for the equilibrium of the body.
Next TopicMechanical Engineering MCQ
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share










