Statistics MCQs1) The runs scored by a batsman in 5 ODIs are 31,97,112, 63, and 12. The standard deviation is
Answer: Option c Explanation: Here, first, we need to find mean 
= 31+97+112+12= 315/5 = 63 Standard deviation = [1/n (x(n)-mean)2]0.5 = 25.79 2) Find the mode of the call received on 7 consecutive day 11,13,13,17,19,23,25
Answer: Option b Explanation: Mode = The value that appears most frequent; here, the number 13 repeated twice. 3) Find the median of the call received on 7 consecutive days 11,13, 17, 13, 23,25,19
Answer: Option d Explanation: 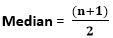
Where, n = number of terms = 7 The median is the middle value of the data sets, so first, we need to arrange the number in ascending order 11,13,13,17,19,23,25 the middle one is 7+1/2 = 4th number so, the 4th number is 17 4) Find the mode and median of the 9 consecutive number 12,7,8,14,21,23,27,7,11
Answer: Option c Explanation: Mode = The value that appears most frequent = 7 which is repeated twice. And, 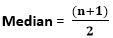
Where n = number of terms = 9 The median is the middle value of the data sets, so first, we need to arrange the number in ascending order 7,7,8,11,12,14,21,23,27 the middle one is 9+1/2 = 5th number so, the 5th number is 12 5) When the Mean of a number is 18, what is the Mean of the sampling distribution?
Answer: Option b Explanation: In sampling distribution, the Mean of a number is equal to the Mean of the sampling distribution; hence the Mean of the number is 18 the Mean of the sampling distribution is 18. 6) If the probability of hitting an object is 0.8, find the variance
Answer: Option b Explanation: Given, P = 0.8 q = 1-p = 1 - 0.8 =0.2 Therefore, mean = q = 0.2 And we know that variance = pq = (0.2) (0.8) = 0.16 7) If the probability that an object dropped from a certain height will strike the ground is 80 percent and if 12 objects are dropped from the same place, find the mean and variance.
Answer: Option q Explanation: Given, p= 80% = 0.8 and q = 1-p = 20% = 0.2 and n= 12 Therefore, Mean= np = (12)(0.8) = 9.6 And, Variance = npq = (9.6)(0.2)= 1.92 8) Find the mean of tossing 4 coins
Answer: Option b Explanation: Here, p = ½ and q = ½ N = 4 Therefore, Mean = np = 4*1/2 = 2 9) Variance of a constant 'x' is
Answer: Option a Explanation: We know that, V(a) = E (x2) - (E(a)2) = x2- x2 = 0 10) E(X) = λ is used for which distribution?
Answer: Option b Explanation: In Poisson's distribution, a positive constant called λ is used, which is the mean and variance of the distribution. The Poisson distribution predicts how many of a certain type of event will occur in a bounded area or during a given period, provided that the events occur independently and cannot occur simultaneously. The events are sometimes called "outcomes" or "observed occurrences." 11) The Mean of a constant 'x' is
Answer: Option c Explanation: The mean of the constant x is x. 12) If P(x) = 0.8 and x = 3, then find the value of E(x)
Answer: Option d Explanation: We know that, E(x) = x P(x) = 0.8*3 = 2.4 13) If P (1) = P (2) in Poisson's distribution, find the value of mean 
Answer: Option a Explanation: We know the formula of Poisson's distribution, 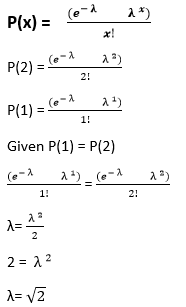
14) If P (1) = λ P (5) in Poisson's distribution, find the value of mean
Answer: Option d Explanation: We know the formula of Poisson's distribution, 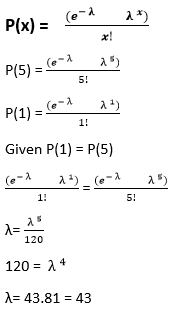
15) Find the expectation of random variable a? 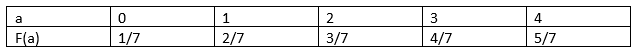
Answer: Option b Explanation: We know that, E(X) = 0(1/7) + 1(2/7) + 2 (3/7) + 3(4/7) + 4(5/7) 0 + 2/7 + 6/7 + 12/7 + 20/7 = 5.71 16) If K is the Mean of Poisson distribution, then the variance is given by
Answer: Option b Explanation: For a discrete probability distribution, the variance is given by the following equation 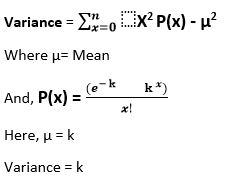
17) If K is the Mean of Poisson distribution, then the standard deviation is given by
Answer: Option a Explanation: A Poisson distribution with mean k is given by Variance = k Therefore, Standard Deviation = √variance = √k 18) Find the arithmetic mean of the set of data: 6,1,5,8, and 10
Answer: Option c Explanation: If we want to calculate the AM, we need to find the total number in the data set. In the given question, total number = 5 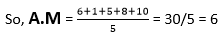
19) Calculate the geometric Mean of 1,3,9,3
Answer: Option c Explanation: In the given question, the total number is 4, so by using the formula to determine the geometric Mean, we have, G.M = (1×3×9×3)1/4 = (81)1/4 = (34)1/4 = 3 20) Find the variance of the given data set: 3,9,5,6,7
Answer: Option d Explanation: If we want to calculate the variance, the first thing you need to do is find the Mean of the given data set, Therefore, 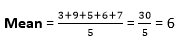
Then, we need to find the Variance V = (3-6)2 + (9-6)2 + (5-6)2 + (6-6)2 + (7-6)2/5 = 9+9+1+0+1 /5 = 20/5 = 4 21) Find the mean, mode and median of the given sets of data: 5,8,12,17,12,14,6,8, 12, and 10
Answer: Option d Explanation: Mean = (5+8+12+13+12+14+6+8+12+10)/ 10 = 10 Mode = Mode is the most repeated value of the given data set. = 12 (12 repeated 3 times in the set of data) For median, first we need to arrange the value in ascending order in the given data set: 5,6,8,8,10,12,12,12,14,17. Here, the numbers 10 and 12 are the middle values. The average of the given number is 12+10/2 = 11. Hence, 11 is the median for the given data set. So, the value of Mean, mode, and median are 10,12,11 22) Find the mean mode and median of the messages received on 7 consecutive days 7,13,5,9,6,5,10
Answer: Option b Explanation: Mean = (9+13+5+9+6+5+9)/7 = 56/7 = 8 Mode = Mode is the most repeated value of the given data set. = 9 (repeated 3 times in the set of data) For median, first, we need to arrange the value in ascending order in the given data set: 5,5,6,9,9,9,13. Here, the number 9 is placed in the middle. Hence, 9 is the median for the given data set. So, the value of Mean, mode, and median are 8,9,9 23) Calculate the range of the given sets of data 7,47,8,42,47,95,42,96,2
Answer: Option b Explanation: Range = Maximum Value - Minimum Value Here, Maximum value in the data sets = 96, and Minimum value = 2 Therefore, Range = 96-2 = 94 24) Find the mean deviation according to the Mean of the given data sets 7,47,8,42,47,95,42,96,3
Answer: Option b Explanation: If we want to calculate the mean deviation according to the Mean. First, we need to calculate the Mean of the given data sets Therefore, Mean = 7+47+8+42+47+95+42+96+3/9 = 43 Now, we need to find the deviation to calculate mean deviation i.e., (43-7) +(47-43) +(43-8) +(43-42) +(47-43) +( 95-47) +(43-42) +(96-43) +(43-3) = 222 So, 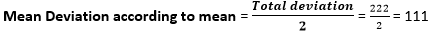
25) Find the mean deviation according to median of the given data sets 7,47,8,42,47,95,42,96,3
Answer: Option c Explanation: If we want to calculate the mean deviation according to the median, first, we need to calculate the median of the given data sets Therefore, to calculate the median, first, we need to arrange the number in ascending order 3,7,8,42,42,47,47,95,96 SO, Median = 42 Now, we need to find the deviation to calculate mean deviation according to median i.e., (42-3) +(47-7) +(42-8) +(42-42) +(42-42) +( 47-42) +(47-42) +(95-42) +(96-42) = So, 
26) Find the variance of the given data sets 7,47,8,42,47,95,42,96,3
Answer: Option c Explanation: If we want to calculate the variance, first, we need to calculate the Mean of the given data sets Therefore, Mean = 7+47+8+42+47+95+42+96+3/9 = 43 Now, we need to find the square of deviation to calculate variance i.e., (43-7)2 +(47-43)2 +(43-8)2 +(43-42)2+(47-43)2 +( 95-47)2 +(43-42)2 +(96-43)2+(43-3)2 = =1296+16+1225+1+16+2304+1+2809+1600 =9268 So, 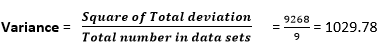
27) Find the standard deviation of the given data sets 7,47,8,42,47,95,42,96,3
Answer: Option c Explanation: If we want to calculate the standard deviation, first, we need to calculate the Mean of the given data sets Therefore, Mean = 7+47+8+42+47+95+42+96+3/9 = 43 Now, we need to find the square root to calculate the variance i.e., (43-7)2 +(47-43)2 +(43-8)2 +(43-42)2+(47-43)2 +( 95-47)2 +(43-42)2 +(96-43)2+(43-3)2 = =1296+16+1225+1+16+2304+1+2809+1600 =9268 
28) Find the coefficient of variation of the given data sets 7,47,8,42,47,95,42,96,3
Answer: Option b Explanation: If we want to calculate the coefficient, we need to calculate the Mean of the given data sets. Therefore, Mean = 7+47+8+42+47+95+42+96+3/9 = 43 Now, we need to find the square root to calculate the variance i.e., (43-7)2 +(47-43)2 +(43-8)2 +(43-42)2+(47-43)2 +( 95-47)2 +(43-42)2 +(96-43)2+(43-3)2 = =1296+16+1225+1+16+2304+1+2809+1600 =9268 So, 
29) Find the value of λ in Poisson's distribution if the probability of getting a tail in a biased coin toss is ¼ when 8 coins are tossed.
Answer: Option a Explanation: Given, Probability (P) = ¼ And we know that, λ = np = (8) × ¼ = 2 30) The Mean of a random variable K is given by equation
Answer: Option a Explanation: The Mean of any data sets refers to the sum of the function in its domain multiplied with random variables' value. Therefore, the Mean is given by E(K), where k is a random variable. 31) Find the Mean of a constant k
Answer: Option a Explanation: Let f(x) be the random variable of the given function X Now, E(k) = ∫kf(x) = kf(x) = k(1) = k 32) Find the Variance of the constant 'K'
Answer: Option b Explanation: Variance (V) = E(k2) - (E(K))2 = k2- k2 = 0 33) Find the variance in a Binomial Distribution, if x, y, and z are the probability of getting success, failure, and a number of trials, respectively.
Answer: Option a Explanation: If we consider a discrete function, the variance is given by the following equation If we consider a discrete function, the variance is given by the following equation Variance(V) = ∑(x=0)Zx2 X(x) - µ2 Here, µ = Mean When we substitute X(x) = zCx Xx y(z-x) in the above equation and µ = zx we get Variance = xyz. 34) Poisson distribution is applied for
Answer: Option c Explanation: Poisson distribution is usually applied for discrete random variables along with Binomial distribution. The Poisson distribution expresses the probability of a given number of events occurring in a fixed interval of time and space if these events occur with a known average rate and independently since the last event. As a result, the distribution is often used in counting processes where the average rate of the events happening is known, and individual events occur independently of each other. 35) If P (1) = λ P (2) in Poisson's distribution, find the value of mean
Answer: Option a Explanation: We know the formula of Poisson's distribution, 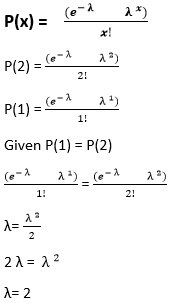
36) calculate the mean the given data set: 3,8,12,17,16,14,6,8, 16, and 10
Answer: Option a Explanation: Mean = Total sum of the number of given data sets/ Total number in data sets (3+8+12+17+16+14+6+8+16+10)/ 10 = 11 37) Find the mode of the given data set: 5,8,12,17,12,12,6,8, 12, and 12
Answer: Option c Explanation: Mode = Mode is the most repeated value of the given data set. = 12 (12 repeated 5 times in the set of data) 38) Find the median of the given data set: 5,8,12,17,2,14,6,8, 13, and 7
Answer: Option c Explanation: For median, first, we need to arrange the value in ascending order in the given data set: 2,5, 6,7, 8,8,12,13,14,17. Here, the numbers 8 and 8 are the middle values. The average of the given number is 8+8/2 = 8. Hence, 8 is the median for the given data set. 39) If the probability of hitting a target is 0.4, find the mean and variance
Answer: Option b Explanation: Given, Probability P = 0.4 q = 1-p = 1 - 0.4 =0.6 Therefore, Mean = q = 0.6 And we know that Variance = pq = (0.4) (0.6) = 0.24 40) Find the arithmetic mean of the set of data: 9,11,10,10,5,15and 10
Answer: Option d Explanation: If we want to calculate the AM, we need to find the total number in the data set. In the given question, total number = 7 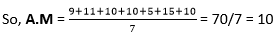
41) Calculate the variance of the given data set: 4,7,6,3,7,3
Answer: Option c Explanation: If we want to calculate the variance, first we need to find the Mean of the given data set, Therefore, 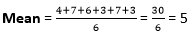
Then, we need to find the Variance (V) = (5-4)2 + (7-5)2 + (6-5)2 + (5-3)2 + (7-5)2 + (5-3)2/6 = 1 + 4 + 1 + 4 + 4 +4/6 = 18/3 = 6 42) If K denotes the expectation, the variance of a random variable X is denoted as?
Answer: Option c Explanation: According to the property of Expectation Variance V(X) = K(X2) - (K(X))2 43) If K is a variance between 0 and 4. Find the value of K(X2)
Answer: Option b Explanation: Integrating f(x) = X2 from 0 and 4 we get the value of K(X2) = 64 44) Find the median of the run made by a player in 5 T20 matches, 55,44, 21, 35, 45.
Answer: Option d Explanation: 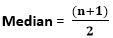
Where n = number of terms = 5 The median is the middle value of the data sets, so first, we need to arrange the number in ascending order 21,35,44,45,55 the middle one is 5+1/2 = 3rd number so, the 3rd number is 44 45) Find the standard deviation of the given data sets 7,2,8,11,6,13,16
Answer: Option b Explanation: If we want to calculate the standard deviation, first, we need to calculate the Mean of the given data sets Therefore, Mean = 7+2+8+11+6+13+16/7 = 63/7 = 9 Now, we need to find the square root to calculate the variance = (Mean - each number of data sets)2 i.e., (9-7)2 +(9-2)2 +(9-8)2 +(9-11)2+(9-6)2 +( 13-9)2 +(16--9)2 =4 + 49 + 1 + 4 + 9 + 16 + 49 =132 So, 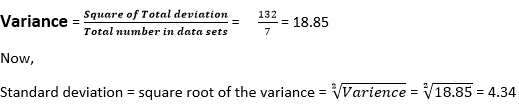
46) Find the coefficient of the given data sets 7,2,8,11,6,13,16
Answer: Option d Explanation: If we want to calculate the standard deviation, first, we need to calculate the Mean of the given data sets Therefore, Mean = 7+2+8+11+6+13+16/7 = 63/7 = 9 Now, we need to find the square root to calculate the variance = (Mean - each number of data sets)2 i.e., (9-7)2 +(9-2)2 +(9-8)2 +(9-11)2+(9-6)2 +( 13-9)2 +(16--9)2 =4 + 49 + 1 + 4 + 9 + 16 + 49 =132 So, 
47) The random variables of A and B have variances 0.4 and 0.6, respectively, and K = 4A - 2B. Find the value of K
Answer: Option d Explanation: Given Variance (A) = 0.4 and Variance (B) = 0.6 And K = 4A - 2B Therefore, Var(K) = Var(4A - 2B) = Var(4A) + Var(2B) = 16 Var(A) + 4 Var(B) Var(K) = 16*0.4 + 4*0.6 = 8.8 48) The mean value of the Hypergeometric distribution is given by the equation
Answer: Option c Explanation: The equation gives the Mean of the Hypergeometric distribution E(X) = n*k/N Where, N denotes the number of trails K denotes the number of success And, N denotes the sample size 49) The Variance of the Hypergeometric distribution is given by the equation
Answer: Option a Explanation: The variance of the Hypergeometric distribution is given by n* k (N-k)*(N-n)/[N2*(N-1)]. Where, n denotes the number of trails K denotes the number of success An, N denotes the sample size. 50) Find the range of the following data sets 61,22,34,17,81,99,42,94.
Answer: Option b Explanation: We know that, Range = Maximum Value - Minimum Value Here, Maximum value in the data sets = 99, and Minimum value = 17 Therefore, Range = 99-17= 82
Next TopicEngineering Mechanics MCQ
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share










