Chi Square test
- In this section, we will learn how to interpret and use the Chi-square test in SPSS. Chi-square test is also known as the Pearson chi-square test because it was given by one of the four most genius of statistics Karl Pearson.
- The Chi-square test is a non-parametric test for testing the significant differences between group frequencies. Often when we work with data, we get the data not always in continuous data format. Data might come in the format of frequencies. For example, how many males, how many females are working in an office. Do they significantly differ from each other, which means there are significantly more males working in a job or office as compared to females.
- For example, suppose we are a government servant, and we want to convey a message that in sectors that are considered hazards like mining and all, there might be more male workers employed than female workers. So, in that case, we might compute a Pearson chi-square test and convey the result that there are significantly more male workers in mining as compared to female workers because the job is of a hazards nature.
- Suppose we are working in an IT sector or in some other sector where an equal number of males and females are supposed to be employed. In that case, we might be interested in proving that there is no significant difference between the number of males and females working in the office. So, in that case, we can use our data and calculate the Pearson chi-square test to covey our result. Since the number of males and females comes in the format of frequency so we cannot apply any parametric tests like ANOVA or t-test. So the chi-square test can be used only when we have our data in the format of frequencies.
- Frequencies can be as simple as the example I gave you as the number of males and the number of females. But if we take multiple groups, in that case, the frequencies might become complex. But chi-square makes our job easy by simply calculating the result. Let us look at this data:
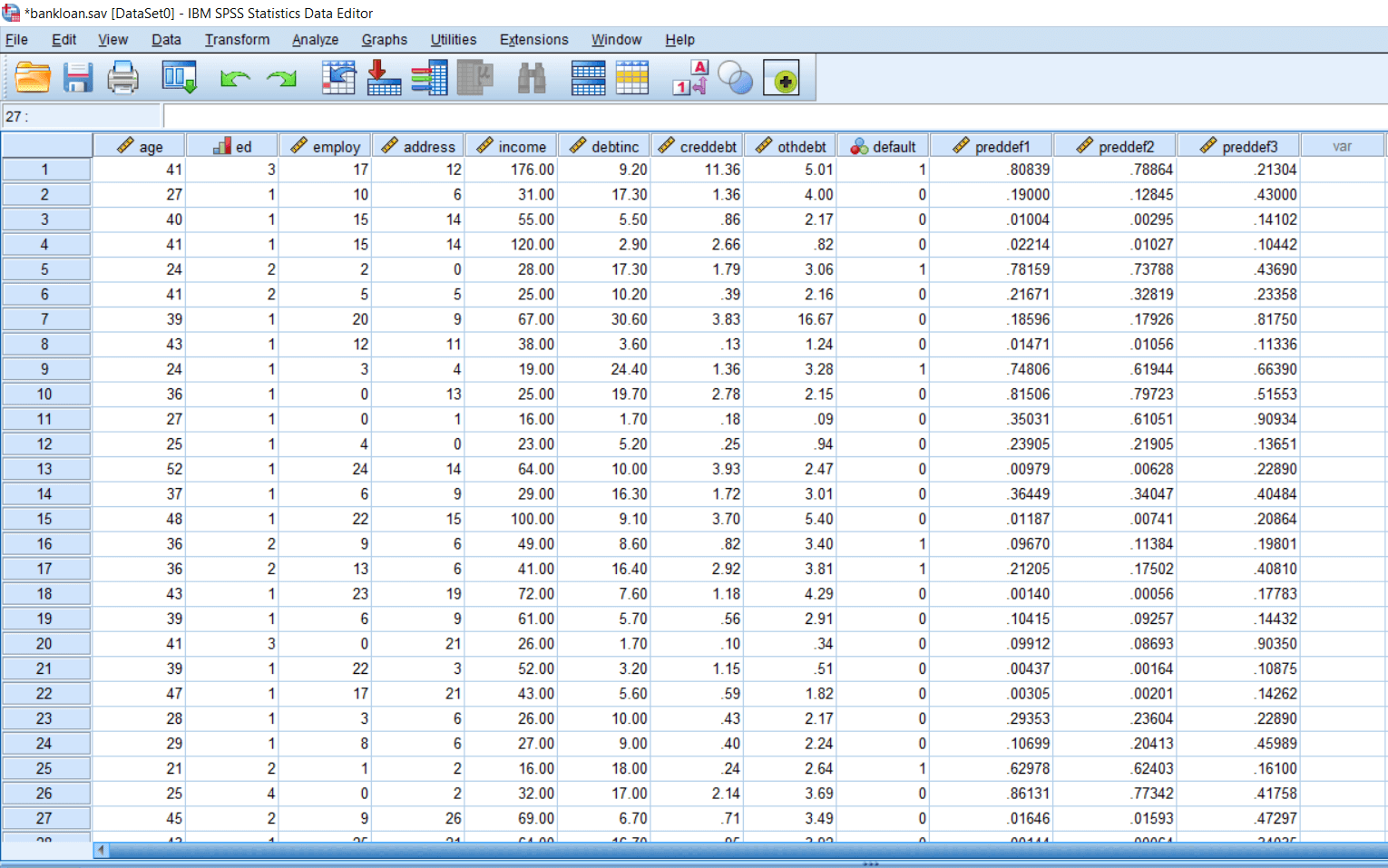
We have taken this data from the SPSS folder. There is bank loan data, and we are having variables like age, education, years with current employer, address, income and other such variables along with the loan default. The researcher might be interested in finding out whether highly educated persons default less loan as compared to persons who are less educated. So we are having default in the format of frequency whether a person defaulted or not. In our case, not default is measured as 0 and default is measured as 1.
For education, we are having various categories ranging from 1 to 5 like this:
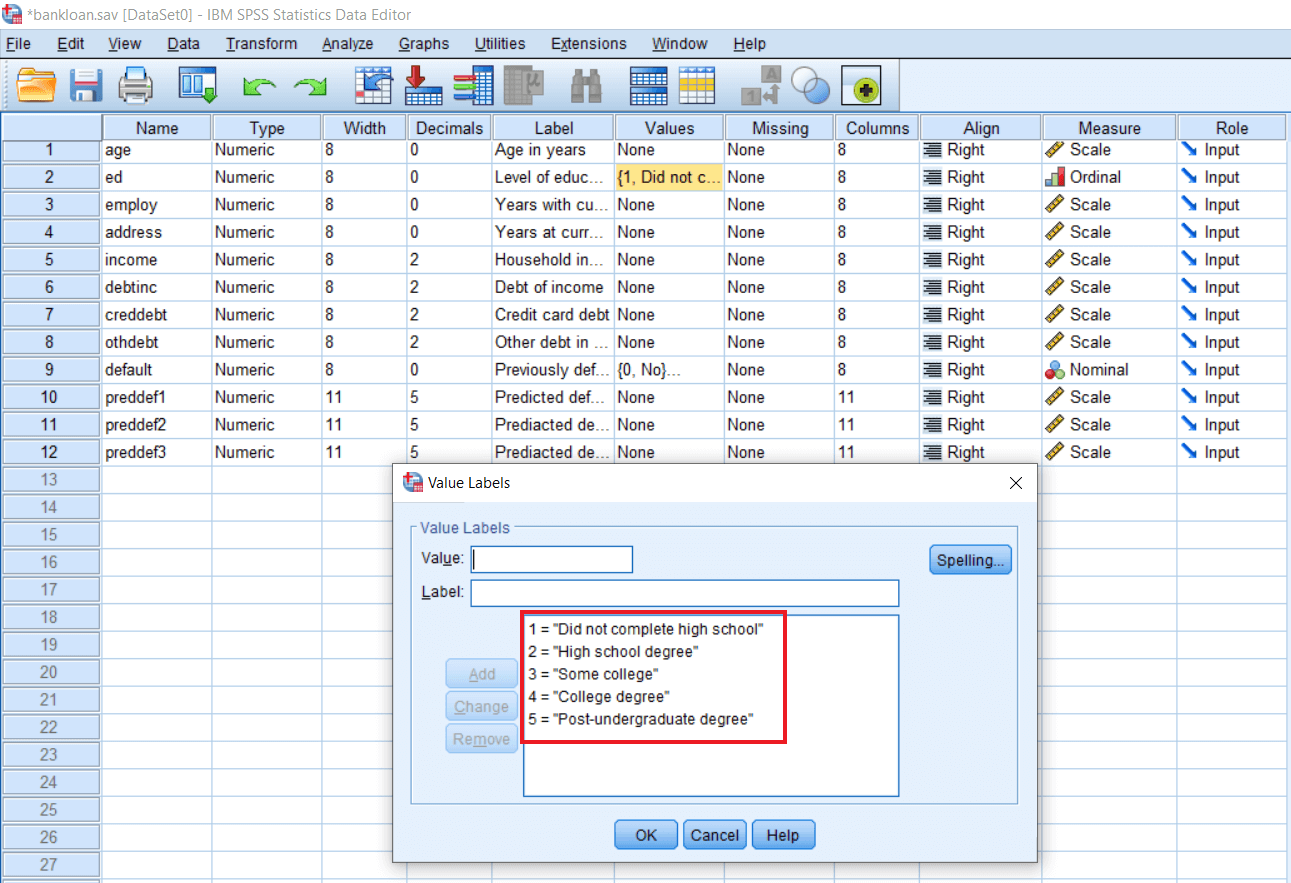
So it could be very interesting to find out if people across different educational categories significantly differ from each other in terms of loan default. In our case, the independent variable is educational qualification or educational category and loan default is our dependent variable. The independent variable and dependent variable are both coming in the format of frequency. So we cannot apply any parametric tests like t-test or ANOVA. In this case, a suitable test will be the Pearson chi-square test.
|



 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now










