Block Diagram in control systemsAny system can be described by a set of differential equations, or it can be represented by the schematic diagram that contains all the components and their connections. However, these methods do not work for complicated systems. The Block diagram representation is a combination of these two methods. A block diagram is a representation of a system using blocks. For representing any system using block diagram, it is necessary to find the transfer function of the system which is the ratio of Laplace of output to Laplace of input. 
Where Then, the system can be represented as Summing Point: When we want to apply a different input signal to the same block then the resultant input signal is the summation of all the inputs. The summation of an input signal is represented by a crossed circle called summing point which is shown in the figure below. 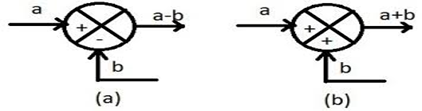
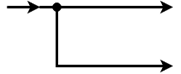
Take off Point: When there is more than one block, and we want to apply the same input to all the blocks, we use a take-off point. By the use of a take-off point, the same input propagates to all the blocks without affecting its value. Representation of same input to more than one block is shown in the below diagram. 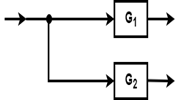
How to draw the block Diagram:Consider a simple R-L circuit 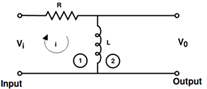
Apply KVL 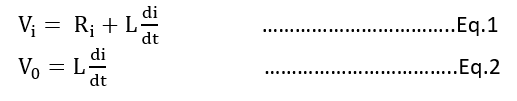
Now taking laplace transform of Eq.1 and Eq.2 with initial condition zero 
From eq.3 and eq.4 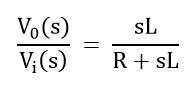
From fig: 
Now taking laplace transform of Eq.5, and Eq.6 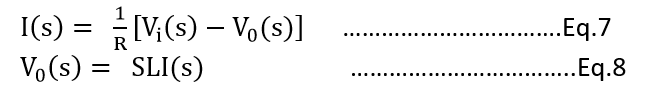
For the right-hand side of eq.5, we will use a summing point. 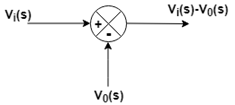
Here the output of summing point is given to the block, and the output of the block is I(s) 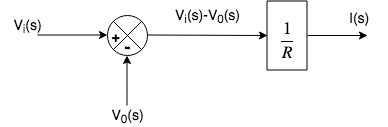
Now the output I(s) is given to another block containing element SL and the output of this block is V0. 
By combining the above two figures, we get the required block diagram. 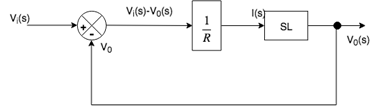
Closed loop control system A system in which a feedback path is there is called a closed-loop control system. In this system, the output is feedback into the error detector and then it is compared with the input signal. The feedback signal can be negative or positive. 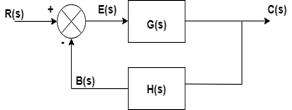
For positive feedback 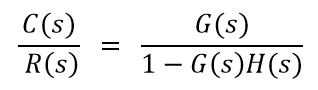
And for negative feedback 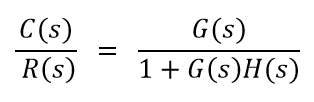
Block diagram reduction rulesRule No.1. Blocks in Cascade When two or more blocks are connected in series, then the resultant block is the product of the individual blocks. 
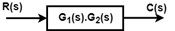
Rule No.2 Blocks in parallel When two or more blocks are connected in parallel, then the resultant block is the sum of the individual blocks. 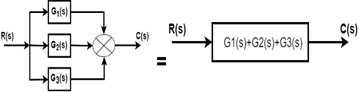
Rule No.3 Moving a take-off point ahead of a block When the take-off point is moved ahead of a block (before the block), then the same transfer function is introduced in the take-off point branch. 
Rule No.4 Moving the take-off point after the block When the take-off point is moved after the block, then a block with reciprocal of a transfer function is introduced in the take-off point branch. 
Rule No.5 Moving a summing point beyond the block 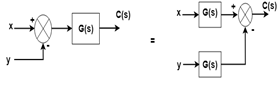
Rule No.6:Moving a summing point ahead of a block 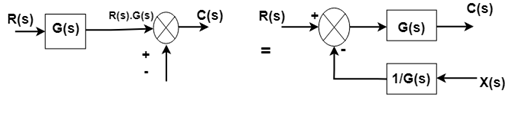
Rule No.7:Interchanging two summing points 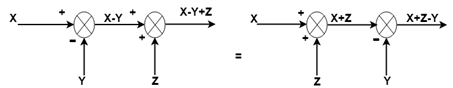
Rule No.8:Moving a take-off point beyond a summing point 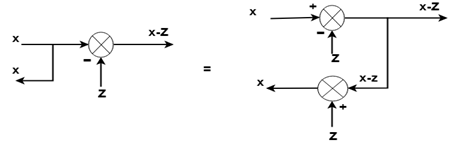
Rule No.9:Moving a take-off point ahead of a summing point 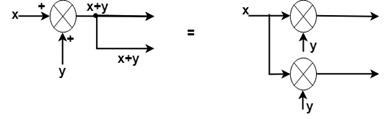
Rule No.10:Eliminating a forward loop 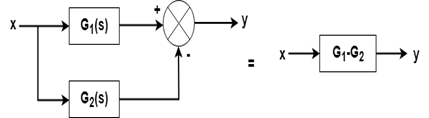
ExampleFind the transfer function of the following by block reduction technique. 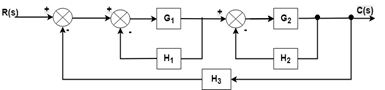
SolutionStep 1: There are two internal closed loops. Firstly, we will remove this loop. 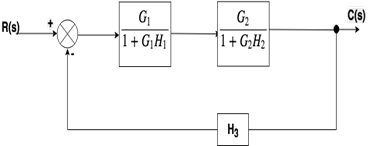
Step 2: When the two blocks are in a cascade or series we will use rule no.1. 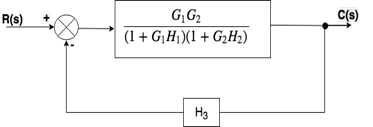
Step 3: Now we will solve this loop. 
Step 4: 
Next TopicSignal flow graphs
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share









