Requirements of a control systemThere are three essential requirements of a control system, namely stability, accuracy, and response. Let's discuss these basic requirements. 1. StabilityFor a particular change in the input signal of the system, the output makes the system's response at a reasonable value. We can also say the value that can be controlled. The response of the stable system is shown below: 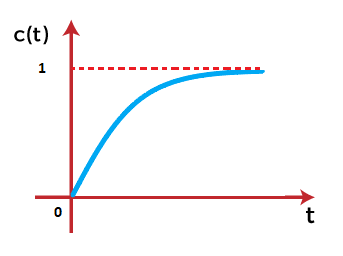
It is the response of the first order system with a unit step input. Its value lies between 0 and 1.
Thus, the position of poles in the s-plane determines the stability of the system. The system based on stability is further categorized as:
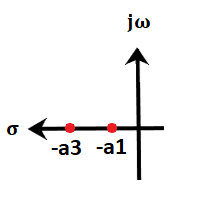
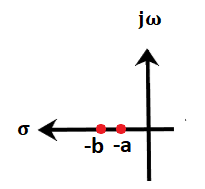
Absolute stable systemIf the system is stable for all the given ranges, it is known as absolute stable system. For example, If the poles of the open loop and closed loop control system lie in the left half of the s-plane, the system is said to be an absolutely stable system. The step response of the absolute stable system is shown below: 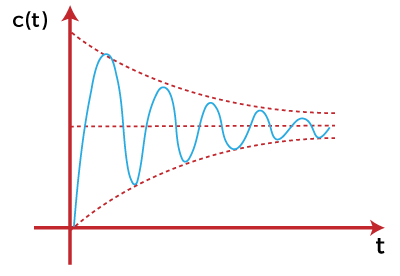
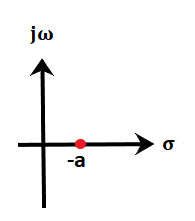
Conditionally stable systemIf the system is stable for certain range of values, it is known as a conditionally stable system. Or If the loop gain of the system lies within a certain range, the system is said to be a conditionally stable system. It means that such type of system exhibits stability only for particular conditions. If these conditions are violated, the system produces unbounded output. The step response of the conditionally stable system is shown below: 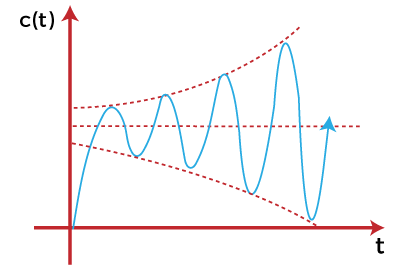
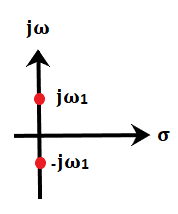
Marginally stable systemA system is said to be marginally stable, if it produces the output with the constant amplitude and constant frequency of oscillations. The input applied to all these systems is bounded. For example, If the poles of the open loop and closed loop control system lie on the imaginary axis, the system is said to be a marginally stable system. These oscillations are known as sustained oscillations. The step response of a marginally stable system is shown below: 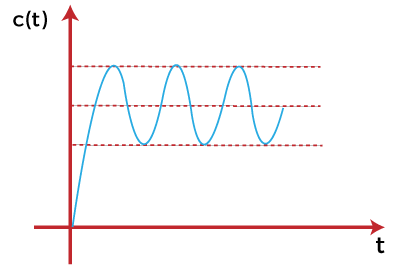
2. AccuracyThe closeness of the measured value to the true value is known as accuracy. The measured value is generally different from the true value. It is one of the important requirements of a control system. It determines the accuracy at which a controlled process reaches the desired value. Accuracy is the initial stage of the development process of the system. It is effective for the prediction of managerial decisions and to analyze accurate data and information. Accuracy also helps find the errors of the measurements, which can be in the form of internal noise or external disturbance. Precision and accuracy are both different words and independent of each other, though both are related to identifying the errors in the system. Precision signifies how the measurements of a system are close to each other, while accuracy tells about the closeness of measurements to the true value. A system can be precise but not accurate, or accurate but not precise, neither accurate nor precise, or can be both accurate and precise. Ideally, a system should be accurate and precise. Hence, these two terms should not be mixed. 3. ResponseThe speed at which an instrument responds to a change in the output signal is known as the system's response. An ideal system has the characteristics of 100% accuracy, perfect stability, and immediate response. All these are not possible in the case of the practical response of a system. |
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share