P, PI, and PID ControllersIntroduction to basic control action and controller Automatic ControllerA device which compares the actual value of plant output with the desired value is called as an Automatic Controller. It determines the deviation of the system and produces the control signal that reduces the deviation to 0 and small value. The manner in which the automatic controller produces the control signal is called the control action. Elements of industrial Automatic Controller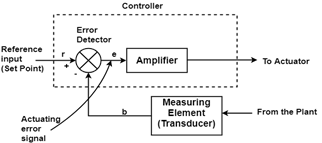
The above controller consists of an error detector and amplifier. The diagram shown above contains a measuring element which is a device that converts the output variable to another variable such as displacement, pressure or electrical signals which can be used for comparing the output to the reference input signal. The reference input (setpoint) of a controller can be converted to reference input of the same units as a feedback signal from the measuring element. So we can say from the above equation that e = r-b, i.e., the deviation is the difference between the controlled variable and set point (reference input) Industrial controller are classified on the basis of control action as
Proportional Control ActionIn a controller, with proportional control action, there is a continuous relationship between the output of the controller (M) (Manipulated Variable) and Actuating Error Signal E (deviation). 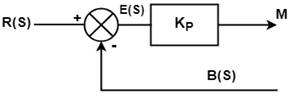

Where, Kp is proportional gain and proportional sensitivity Integral Control Action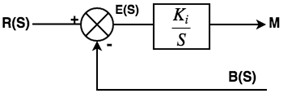
In a controller, with integral control action, the output of the controller is changed at a rate which is proportional to the actuating error signal. E (t) Mathematically 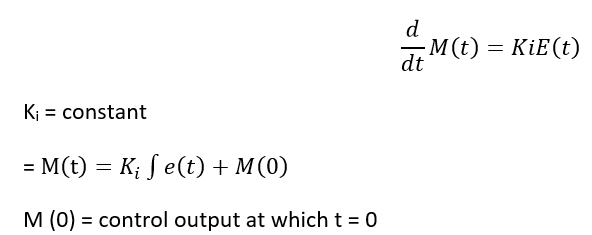
Laplace transform 
It is also known as reset controller and the above equation is the ratio of transfer function of integral controller. Derivative Control action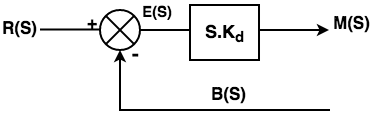
In controller with derivative control action the output of the controller depends on the rate of change of the e(t) 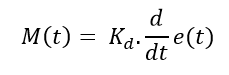
Where Kd is derivative control action By taking Laplace, 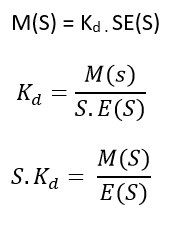
Next TopicControl system Compensators
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share









