State variable analysis: Examples with explanation

Let's first discuss a small introduction about the state variables before proceeding with the examples.

State means a set of variables whose knowledge helps us to predict the behaviour of the control system. The state variable with the input functions provides the future state and the output of the system. The elements of the state variable analysis include state vector, state space, state equations, and the state variable representation.

The state variables are the n variables needed to describe the system's behaviour, and the state axis is the area where coordinate axes are described. Similarly, state equations are the set of n equations, and state variable representation is described in terms of state variables, such as x1(t), x2(t), and so on. The system's input, output, initial conditions, etc., is described in terms of these elements.

Here, we will discuss the examples in the form of Multiple Choice Questions because they will help us in the competitive exams.

Example 1: A system is described by the state equation X' = AX + BU. The output is given by Y = CX, where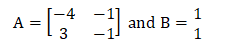

And C = [1 0]

The transfer function of the system is:

1. s/s² + 5s + 7
2. 2s/s² + 5s + 7
3. 1/s² + 5s + 7
4. s/s² + 3s + 5

Answer: (a) s/s² + 5s + 7

Explanation: The equation to find the transfer function of the system is given by:

C [SI - A]^-1B + D

Where,

I is always an identity matrix.

Computing the values of A, B, I, and C in the above equation, we get:

Transfer function = C [SI - A]^-1B + D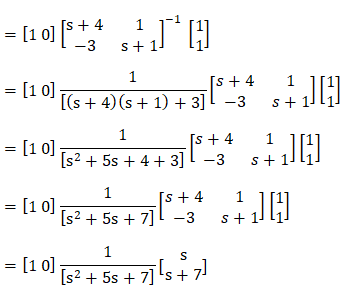

= s/s² + 5s + 7

Thus, the correct answer is an option (a).

Example 2: Find the sum of the Eigen values of the matrix given below: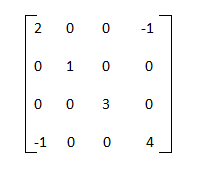

1. 15
2. 12
3. -10
4. 10

Answer: (d) 10

Explanation: The shortcut approach to find the sum of the Eigen values is to add the elements present in the diagonal of the given matrix.

The diagonal elements are 2, 1, 3, and 4. It sum is equal to 2 + 1 + 3 + 4 = 10

Hence, the correct answer is 10.

Example 3: A system represented by the equations is given by: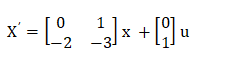

And Y = [1 0]

Find the equivalent transfer function of the system.

1. s/s² + 3s + 3
2. 1/s² + 3s + 2
3. 5/s² + 5s + 2
4. 2/s² + 3s + 5

Answer: (b) 1/s² + 3s + 2

Explanation: The equation to find the transfer function of the system is given by:

C [SI - A]^-1B + D

Where,

I is always an identity matrix.

Computing the values of A, B, I, and C in the above equation, we get:

Transfer function = C [SI - A]^-1B + D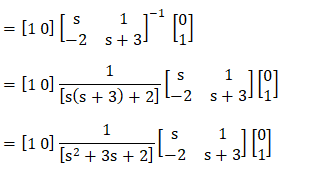

= 1/s² + 3s + 2

Example 4: The observability condition in the state space representation can be determined with the condition given by:

1. [C^T A^TC^T]
2. [B^T A^TB^T]
3. [A^T A^TC^T]
4. None of these

Answer: (a) [C^T A^TC^T]

Explanation: The observability condition can be determined from the condition [C^T A^TC^T].

Example 5: The system model given by the equation is: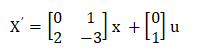

Y '= [1 1] x

1. Controllable
2. Observable
3. Both (a) and (b)
4. Neither (a) nor (b)

Answer: (c) Both (a) and (b)

Explanation: We know that the equation is represented in the form of AX + BU.

By comparing, we get: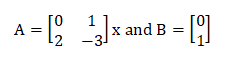

C = [1 1]

The controllability of the given state equation can be checked by forming the matrix [B AB]. The observability of the given state equation can be checked by forming the matrix [C^T A^TC^T]. If the determinant of these matrixes is not equal to zero, it is said to observable or controllable.

The matrix so formed for the controllability is given by:

[B AB]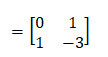

The determinant of the above matrix is: 0 x -3 - 1 = -1

It is not equal to 0. Hence, the matrix is controllable.

Now, let's check for observability.

The matrix so formed for the observability is given by:

[C^T A^TC^T]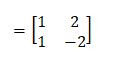

The determinant of the above matrix is: 1 x -2 - 2 = -4

It is not equal to 0. Hence, the matrix is observable.

Thus, the system model described by the given state equation is both controllable and observable.

Example 6: The state of a system equation can be written in the form of:

1. First order differential equation
2. Second order differential equation
3. Third order differential equation
4. None of the above

Answer: (a) First order differential equation

Explanation: The state of a system equation is written in the form of first order differential equation using the state variables x1, x2, x3 ? xn.

Example 7: A LTI system is described by the state model given by: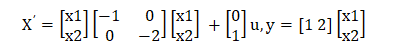

Find if the system is:

1. Completely controllable
2. Completely observable
3. Not completely controllable but completely observable
4. Not completely observable but completely controllable

Answer: (c) Not completely controllable but completely observable

Explanation: The controllability of the given state equation can be checked by forming the matrix [B AB]. The observability of the given state equation can be checked by forming the matrix [C^T A^TC^T].

We will use the above two conditions to determine controllability and observability.

We can check either the determinant or the rank of the formed matrix. If the determinant of these matrixes is not equal to zero, it is said to observable or controllable. If the rank of the matrix is equal to its order, it is said to be observable or controllable.

Let's start.

By comparing the given state model, the parameters are: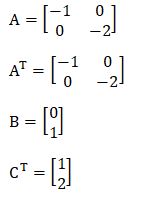

Now, the matrix [B AB] is given by: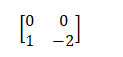

The determinant of the above matrix is equal to 0. Hence, it is not completely controllable. We can also say that the rank of the matrix is not equal to its order (2).

Now, the matrix [C^T A^TC^T] is given by: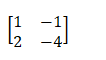

The determinant of the above matrix is not equal to 0. Hence, it is completely observable. We can also say that the rank of the matrix is equal to its order (2).

Thus, the given state model is completely observable but not completely controllable.