Mathematical modeling and representation of a physical system

A physical system is a system in which physical objects are connected to perform an objective. We cannot represent any physical system in its real form. Therefore, we have to make assumptions for analysis and synthesis of systems. An idealized physical system is called a physical model. A physical system can be modeled in different ways depending upon the problem and required accuracy with which we have to deal.

For example

We can model an electronic amplifier as an interconnection of linear lumped elements, and in case the stress is on distortion analysis then same can be pictured as nonlinear elements.

When we have obtained the physical model of a physical system the next step is to obtain the mathematical model which is called the mathematical representation of the physical model.

Before proceeding let us know, what is the meaning of modeling of the system?

The process of drawing the block diagram for mechanical and electrical systems to find the performance and the transfer functions is called the mathematical modeling of the control system.

There are two types of physical system:

1. Mechanical system.
2. Electrical system.

Mathematical modeling of the Mechanical system

There are two types of mechanical systems which we have to study.

1. Translational or Linear system.
2. Rotational system.

Translational or Linear system: The motion that takes place along a straight line is called a translational motion. There are three different types of forces that we have to study.

1. Inertia Force: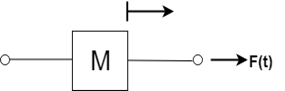

Consider a body of mass 'M' and acceleration 'a' then according to newton's second law of motion:

In terms of velocity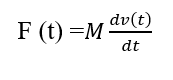

In terms of displacement the above equation can be expressed as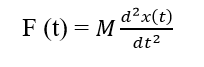

2. Damping Force: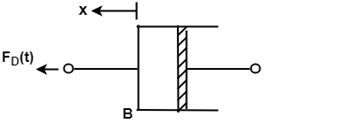

For viscous friction, we assume that the damping force is proportional to the velocity.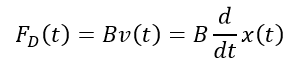

Where B = Damping Coefficient Unit of B = N/m/sec.

3. Spring Force: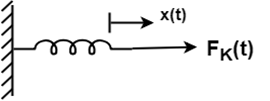

A spring has potential energy. The restoring force of a spring is proportional to the displacement.

    FK (t)∝x(t)=Kx(t)
                  Fk (t)=k∫v (t)dt

Where

Rotational component

Moment of inertia or torque

Moment of inertia.

Rotational System:When the motion of a body takes place about a fixed axis, this type of motion is known as rotational motion. There are three types of torques that resist the rotational motion.

1. Inertia Torque: The property of an element that stores the kinetic energy of rotational motion is called inertia (J). The inertia Torque T₁ is the product of the moment of inertia J and angular acceleration α (t).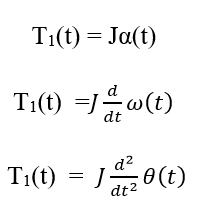

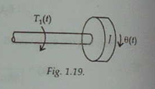
Where

Unit of Torque = N-m

2. Damping Torque: The product of angular velocity ω and damping coefficient B is known as Damping Torque T_D(t).

3. Spring Torque: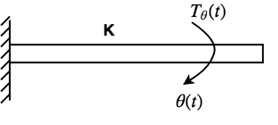

Spring Torque Tθ(t) is the product of torsional stiffness and angular displacement.

Unit of K = N-m/rad.

By comparing equations, we get an analogous system:

Mathematical modeling of the Electrical system

Analogous System

Consider a series RLC circuit.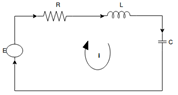

Apply Kirchhoff's voltage law

In terms of charge equation becomes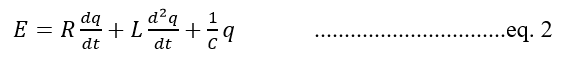

Now consider a parallel RLC circuit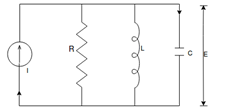

Now apply Kirchhoff's current law

In terms of magnetic flux linkage, the above equation becomes Since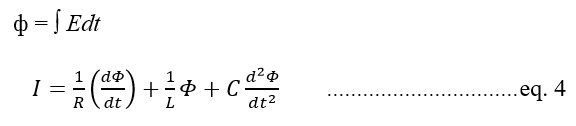

Force Current Analogy