DAG representation for basic blocksA DAG for basic block is a directed acyclic graph with the following labels on nodes:
Algorithm for construction of DAGInput:It contains a basic block Output: It contains the following information:
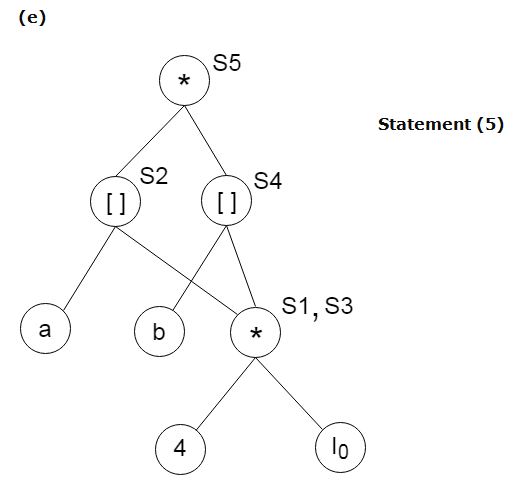
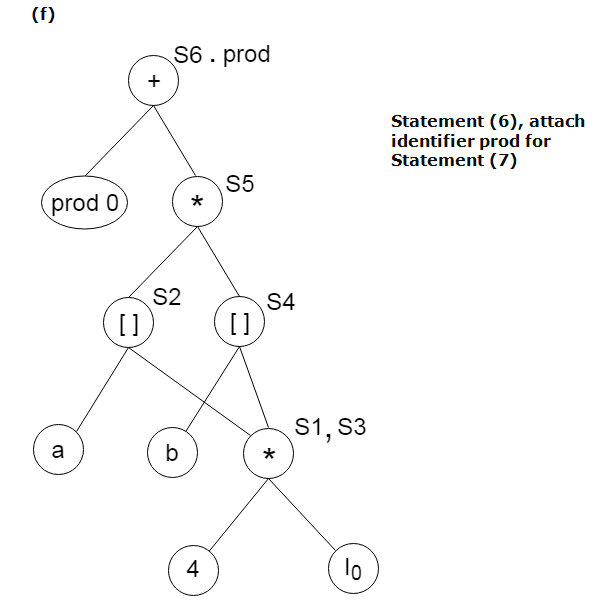
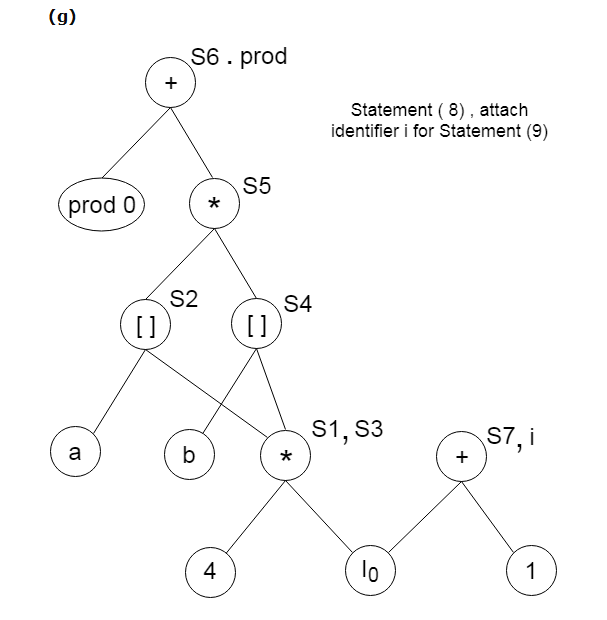
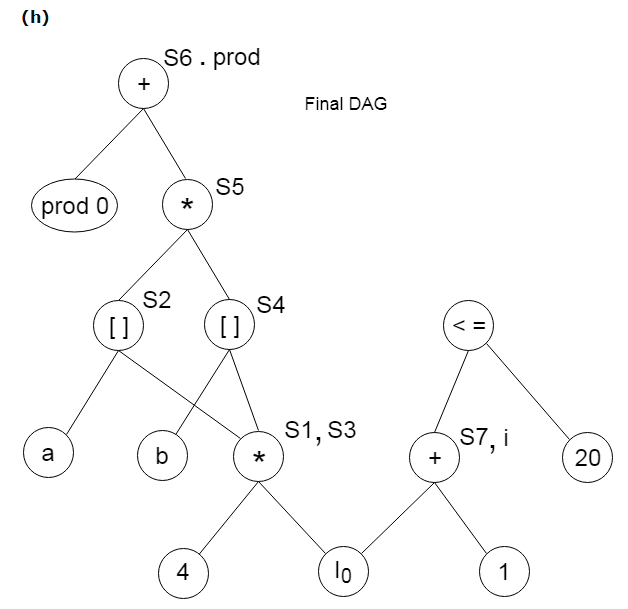
Method:Step 1: If y operand is undefined then create node(y). If z operand is undefined then for case(i) create node(z). Step 2: For case(i), create node(OP) whose right child is node(z) and left child is node(y). For case(ii), check whether there is node(OP) with one child node(y). For case(iii), node n will be node(y). Output: For node(x) delete x from the list of identifiers. Append x to attached identifiers list for the node n found in step 2. Finally set node(x) to n. Example:Consider the following three address statement: Stages in DAG Construction: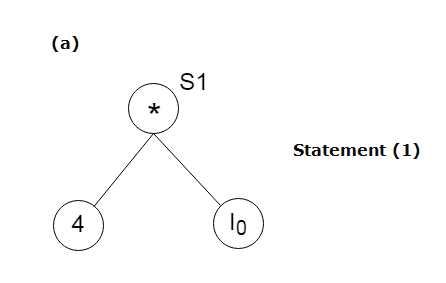
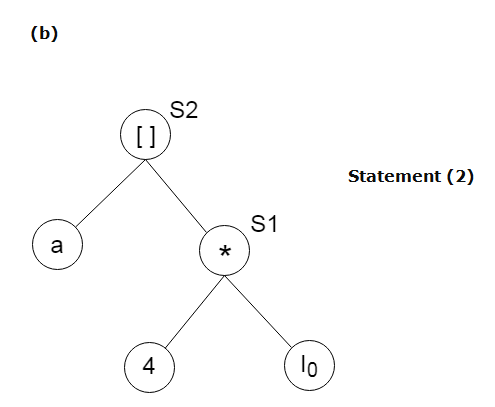
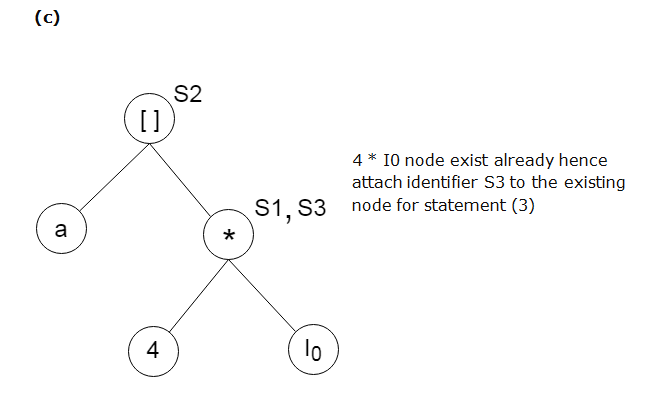
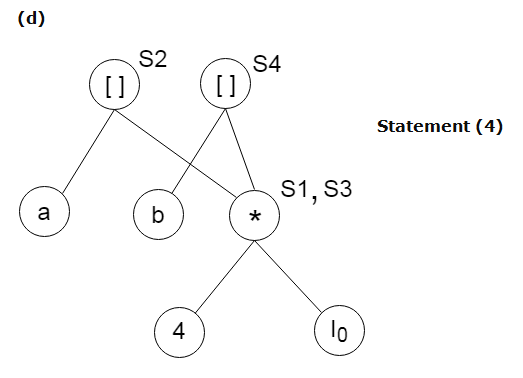
Next TopicData Flow Analysis
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share









