Eliminating Ambiguity of a Context-Free Grammar

In the Syntactic analysis phase of compilation, the programming language constructs are specified in a context-free grammar. Context-free grammar can generate all the possible strings of a formal language. Given a grammar, all the strings (a string of tokens from lexical analysis) that the grammar can generate are said to be well-formed and to check this, the parser builds a parse tree.

If the grammar is ambiguous, not one parser can accept it. What is ambiguity?

Let us take little steps:

Everything you need to understand about Context free grammar:

Where:

V: Non-terminals (S, A, B, C...)

T: Terminals-> String symbols (a, b, c...)

P: Production rules (Non-terminal -> 0 or more terminals or non-terminals.

E.g., A -> aA/a)

S: Start symbol (One non-terminal)

Here are some terms to understand before writing grammar:

Derivation: Replacing a Non-Terminal from the body of the production rules to obtain strings. These Terminal strings make the language of the grammar.

For example:

Language: All the strings with balanced opening and closing parenthesis.

Grammar: S -> (S) S/ε

The Non-terminals in the body of the production: S

Suppose, given input string is w = (((())))

Derivation: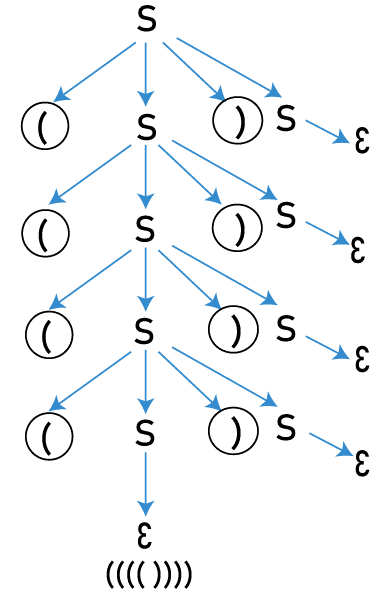

This representation is called a Derivation Tree/ Parse Tree.

If there is more than one parse tree for an input string, the grammar is said to be "Ambiguous".

Note: Every grammar will have one leftmost and one right-most derivation tree. An Ambiguous grammar is a grammar with either more than one leftmost derivation tree or more than one right-most derivation tree.

Generally, the parse tree generated in the syntax analysis is passed to the rest of the compilation, but if a string has more than one parse tree, the compiler won't be able to figure out which parse tree to consider.

Let us take an example:

Grammar:

Input string: id + id* id

The leftmost derivation can be done in two ways: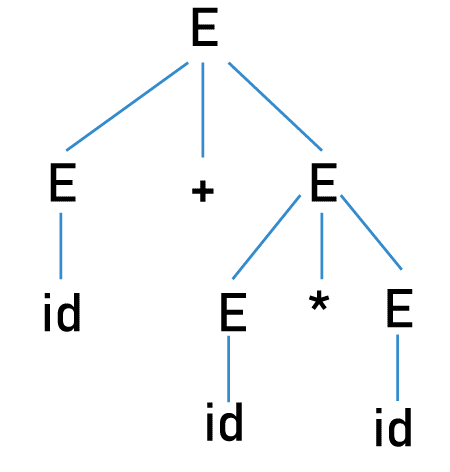

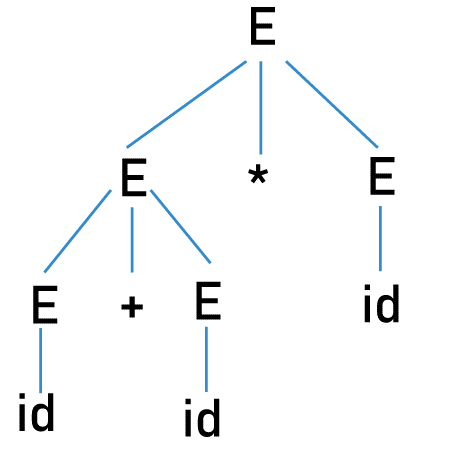
For the given input string, we got two leftmost derivation trees. We need to eliminate the ambiguity in the grammar.

Eliminating the ambiguity in CFG grammar:

Ambiguity from all grammar cannot be eliminated. No direct and official algorithm can determine whether the given grammar is ambiguous. We need to check by building all the possible parse trees. We can use Precedence and Associativity to remove the ambiguity from some grammar.

Let us take an example:

Grammar:

Here var can be any variable, and const can be any constant value. A string a - b - c has two leftmost derivations: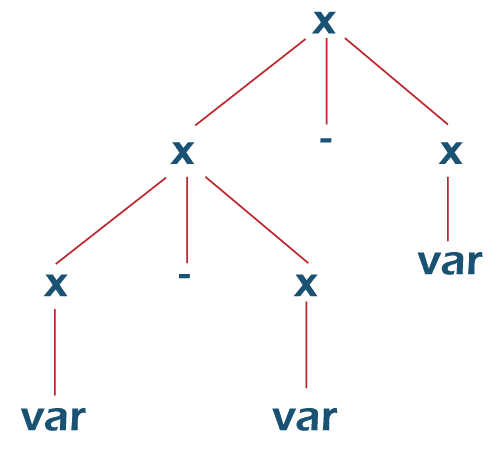

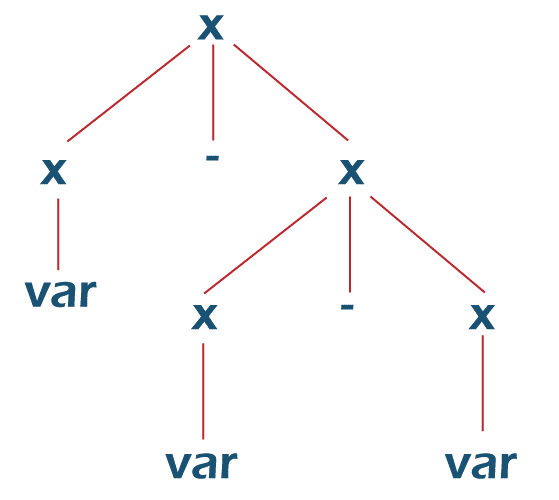
For example, if we take the values a = 2, b = 3 and c = 4:

a - b - c = 2 - 3 - 4 = -5

In the first derivation tree, according to the order of substitution, the expression will be evaluated as:

(a - b) - c = (2 - 3) - 4 = -1 -4 = -5

In the second derivation tree: a - (b - c) = 2 - (3 - 4) = 2 - -1 = 3

Observe that both parse trees aren't giving the same value. They have different meanings. In the above example, the first derivation tree is the correct parse tree for grammar.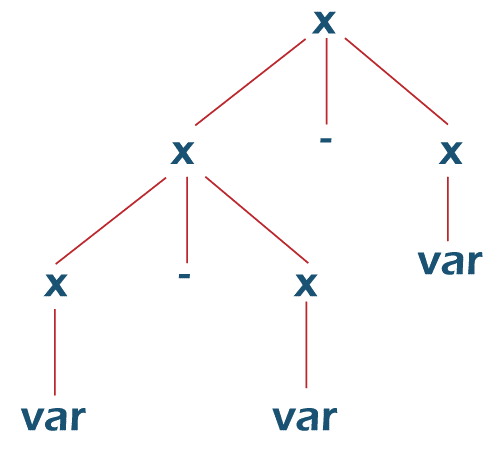

(a - b) - c. Here there are two same operators in the expression. According to mathematical rules, the expression must be evaluated based on the associativity of the operator used. In the above example, the operator is -, which gives left-to-right associativity. Hence, the first derivation tree is the correct parse tree.

So, for the left to right-associative operators, the parse tree has to be left associative-The Non-terminals on the left sub-tree must be derived first and then the right sub-tree.

Note: For the right-to-left associative operators like ^, the grammar has to be made right-associative because, for these expressions, the order of evaluation must be from right to left.

Now, let us convert the grammar into unambiguous grammar:

We need to make the grammar left-recursive. We need to place a random non-terminal in place of the right Non-terminal:

Now, for the string a - b - c:

Now, what if the grammar is:

This grammar will give two leftmost derivation trees for the string, id + id * id*.

We can't use associativity here as there are two different operators, + and *. Hence, we need to use "Precedence".

In the string:

The order of evaluation must be: id + (id * id) as * has more precedence than +. The operator with the highest priority must be evaluated first. Hence, the operators with high priority are to be arranged in the lower levels of the parse tree.

If id = 2:

If + id * id = 2 + 2 * 2 = 6

For the first derivation tree: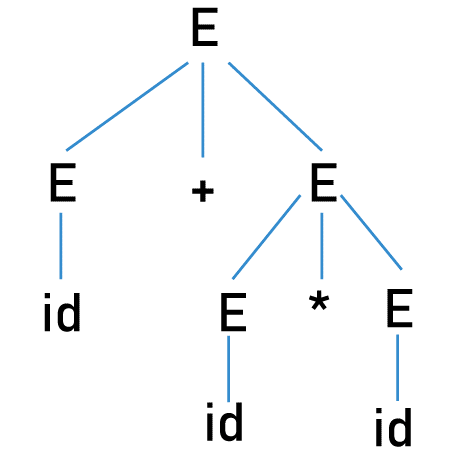

id + (id * id) = 2 + (2 * 2) = 2 + 4 = 6

For the second derivation tree: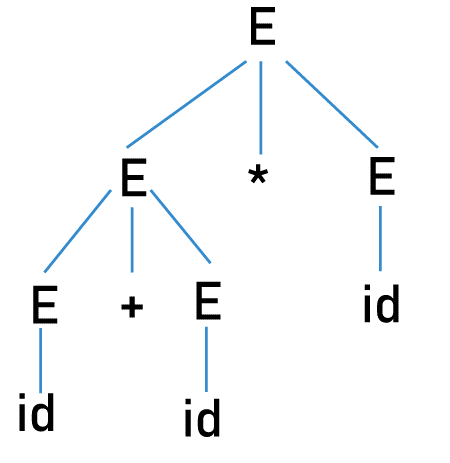

(id + id) * id = (2 + 2) * 2 = 4*2 = 8

Hence, the first derivation tree is the correct parse tree.

Converting into unambiguous grammar:

We should write the grammar so that all the highest priority operators stay in lower levels. Every production should follow a recursion based on the associativity of the operator used.

• +, -, *, / are left associative operators. Hence, the productions using these operators must follow left recursion
• ^ and = are right-associative operators. Hence, the productions using these operators must follow the right recursion.

Given grammar:

Precedence: * has the highest priority than +. Hence, it should be at a lower level. So, we need to start with +

Assocaitivity: + and * both are left assocaitive

Parse tree:

Now, finally, let us take another example:

First, determine whether the given grammar is ambiguous.

Given a string id + id * id ^ id

E -> E + E

id + E * E

id + id * E

id + id * E^E

id + id * id ^ id

E -> E * E

E + E * E

id + E * E

id + id * E ^ E

id + id * id ^ id

More than one left most derivation trees.

Operators: +, * and ^

Precedence: ^ > * > +

Associativity:

+, * -> left to right

^ -> right to left

• We need to arrange the grammar so that the production with ^ and * are in the lower levels of the parse tree, and every production must follow the associativity of its operator.

Grammar:

E -> E + P/P

P -> P * Q/Q

Q -> R ^ Q/R (Right associative)

R -> id

Parse Tree:

Evaluation:

If id = 2: id + id * id ^ id = 2 + 2 * 2² = 2 + 2 * 4 = 16

Important points to remember

1. When checking if the grammar is ambiguous, we must consider a string carefully. Some strings of ambiguous grammar might not be ambiguous.
2. In the process of eliminating ambiguity, do not alter the grammar. We shouldn't change the original language and use non-terminals so that the grammar's meaning isn't altered.