Backpropagation Process in Deep Neural NetworkBackpropagation is one of the important concepts of a neural network. Our task is to classify our data best. For this, we have to update the weights of parameter and bias, but how can we do that in a deep neural network? In the linear regression model, we use gradient descent to optimize the parameter. Similarly here we also use gradient descent algorithm using Backpropagation. For a single training example, Backpropagation algorithm calculates the gradient of the error function. Backpropagation can be written as a function of the neural network. Backpropagation algorithms are a set of methods used to efficiently train artificial neural networks following a gradient descent approach which exploits the chain rule. The main features of Backpropagation are the iterative, recursive and efficient method through which it calculates the updated weight to improve the network until it is not able to perform the task for which it is being trained. Derivatives of the activation function to be known at network design time is required to Backpropagation. Now, how error function is used in Backpropagation and how Backpropagation works? Let start with an example and do it mathematically to understand how exactly updates the weight using Backpropagation. 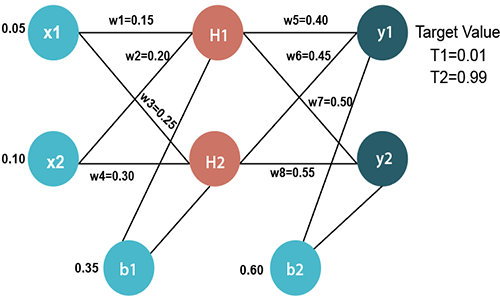
Input valuesX1=0.05 Initial weightW1=0.15 w5=0.40 Bias Valuesb1=0.35 b2=0.60 Target ValuesT1=0.01 Now, we first calculate the values of H1 and H2 by a forward pass. Forward PassTo find the value of H1 we first multiply the input value from the weights as H1=x1ūw1+x2ūw2+b1 To calculate the final result of H1, we performed the sigmoid function as 
We will calculate the value of H2 in the same way as H1 H2=x1ūw3+x2ūw4+b1 To calculate the final result of H1, we performed the sigmoid function as 
Now, we calculate the values of y1 and y2 in the same way as we calculate the H1 and H2. To find the value of y1, we first multiply the input value i.e., the outcome of H1 and H2 from the weights as y1=H1ūw5+H2ūw6+b2 To calculate the final result of y1 we performed the sigmoid function as 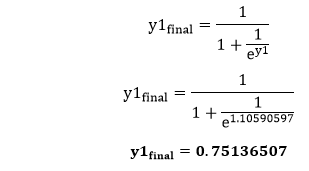
We will calculate the value of y2 in the same way as y1 y2=H1ūw7+H2ūw8+b2 To calculate the final result of H1, we performed the sigmoid function as 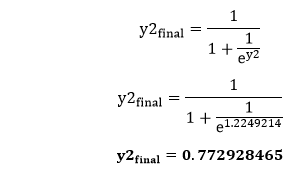
Our target values are 0.01 and 0.99. Our y1 and y2 value is not matched with our target values T1 and T2. Now, we will find the total error, which is simply the difference between the outputs from the target outputs. The total error is calculated as 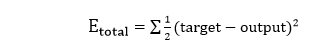
So, the total error is 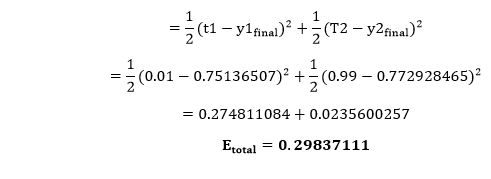
Now, we will backpropagate this error to update the weights using a backward pass. Backward pass at the output layerTo update the weight, we calculate the error correspond to each weight with the help of a total error. The error on weight w is calculated by differentiating total error with respect to w. 
We perform backward process so first consider the last weight w5 as 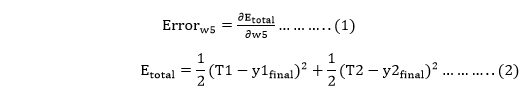
From equation two, it is clear that we cannot partially differentiate it with respect to w5 because there is no any w5. We split equation one into multiple terms so that we can easily differentiate it with respect to w5 as 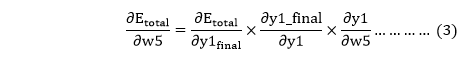
Now, we calculate each term one by one to differentiate Etotal with respect to w5 as 
Putting the value of e-y in equation (5) 
So, we put the values of 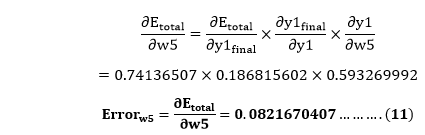
Now, we will calculate the updated weight w5new with the help of the following formula 
In the same way, we calculate w6new,w7new, and w8new and this will give us the following values w5new=0.35891648 Backward pass at Hidden layerNow, we will backpropagate to our hidden layer and update the weight w1, w2, w3, and w4 as we have done with w5, w6, w7, and w8 weights. We will calculate the error at w1 as 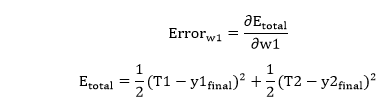
From equation (2), it is clear that we cannot partially differentiate it with respect to w1 because there is no any w1. We split equation (1) into multiple terms so that we can easily differentiate it with respect to w1 as 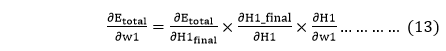
Now, we calculate each term one by one to differentiate Etotal with respect to w1 as 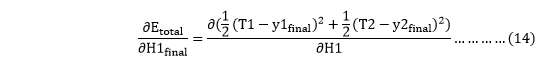
We again split this because there is no any H1final term in Etoatal as 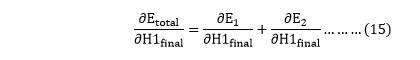
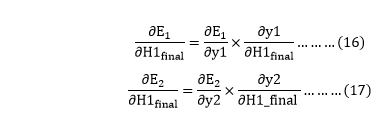
We again Split both 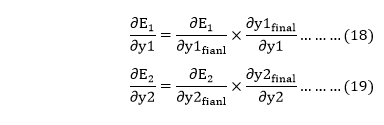
Now, we find the value of From equation (18) 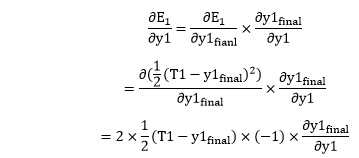
From equation (8) 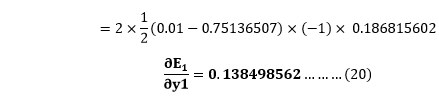
From equation (19) 
Putting the value of e-y2 in equation (23) 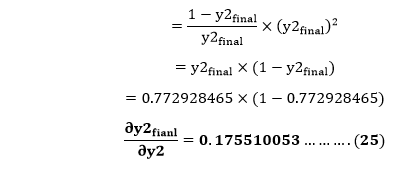
From equation (21) 
Now from equation (16) and (17) 
Put the value of 
We have 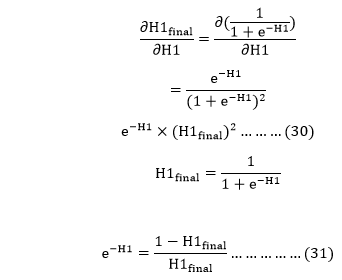
Putting the value of e-H1 in equation (30) 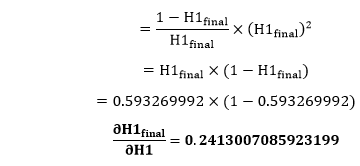
We calculate the partial derivative of the total net input to H1 with respect to w1 the same as we did for the output neuron: 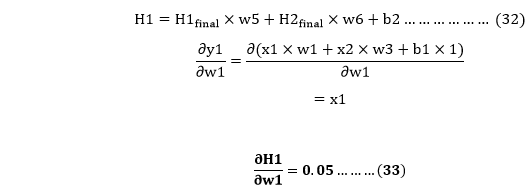
So, we put the values of 
Now, we will calculate the updated weight w1new with the help of the following formula 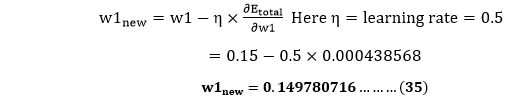
In the same way, we calculate w2new,w3new, and w4 and this will give us the following values w1new=0.149780716 We have updated all the weights. We found the error 0.298371109 on the network when we fed forward the 0.05 and 0.1 inputs. In the first round of Backpropagation, the total error is down to 0.291027924. After repeating this process 10,000, the total error is down to 0.0000351085. At this point, the outputs neurons generate 0.159121960 and 0.984065734 i.e., nearby our target value when we feed forward the 0.05 and 0.1.
Next TopicImplementation of Deep Neural Network
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share




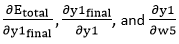 in equation no (3) to find the final result.
in equation no (3) to find the final result.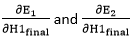 will again split because in E1 and E2 there is no H1 term. Splitting is done as
will again split because in E1 and E2 there is no H1 term. Splitting is done as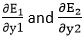 because there is no any y1 and y2 term in E1 and E2. We split it as
because there is no any y1 and y2 term in E1 and E2. We split it as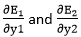 by putting values in equation (18) and (19) as
by putting values in equation (18) and (19) as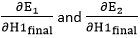 in equation (15) as
in equation (15) as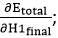 we need to figure out
we need to figure out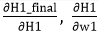 as
as in equation (13) to find the final result.
in equation (13) to find the final result.




