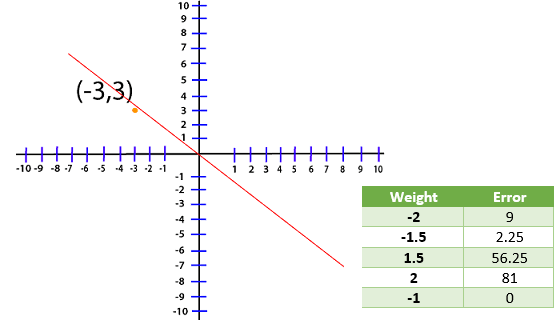
Loss Function in PyTorch

In the previous topic, we saw that the line is not correctly fitted to our data. To make it best fit, we will update its parameters using gradient descent, but before this, it requires you to know about the loss function.

So, our goal is to find the parameters of a line that will fit this data well. In our previous example, the linear function will initially assign random weight and bias parameter to our line with the following parameter.

This line does not represent our data well. We need some optimization algorithm that will adjust these parameters based on the total error until we end up with a line containing suitable parameters.

Now, how do we determine these parameters?

For a good understanding, we limit our discussion to a single data point.

The error is determined by subtracting the prediction at that point from the actual y value.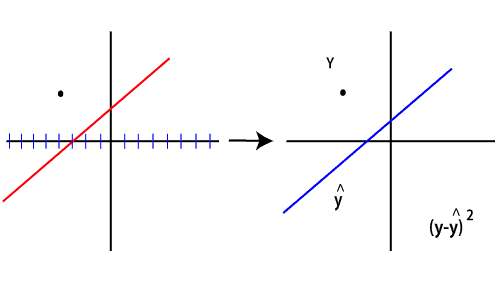

The closer the prediction is to the value, the smaller the error. The prediction as you already know can be written as

Ax1+b

However, we are dealing with a single dot. So that an infinite amount of line can be drawn through it. For this, we remove the bias. Removing this extra degree of freedom for now, and we cancel it out by fixing the bias value zero.

(y-y^)2
(y-(Ax+b))2
(y-(Ax+0))2
(y-Ax)2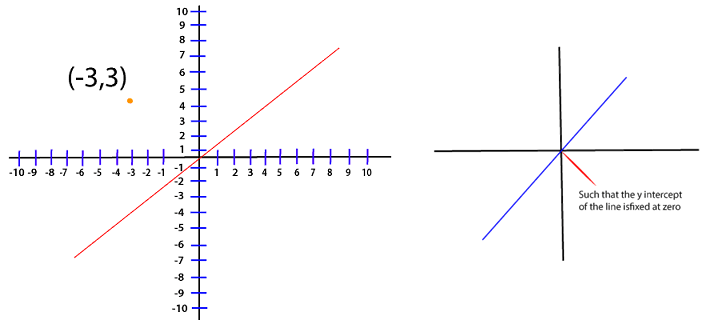

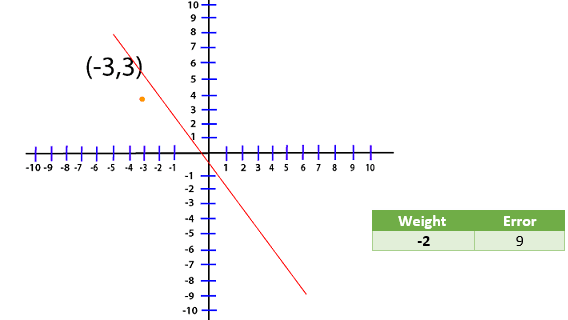
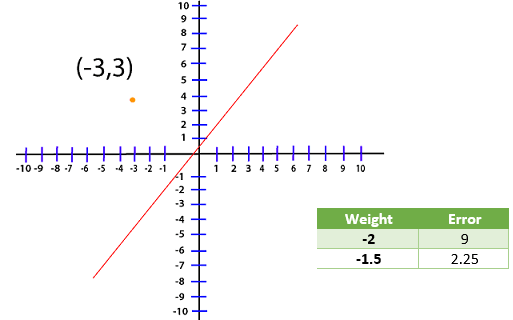
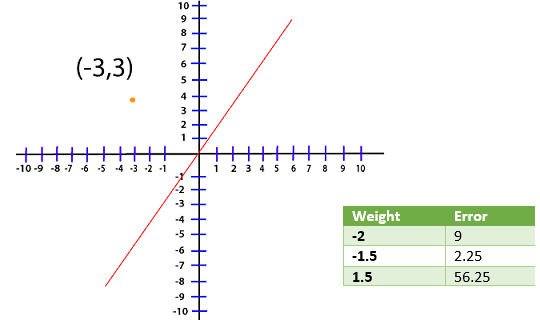
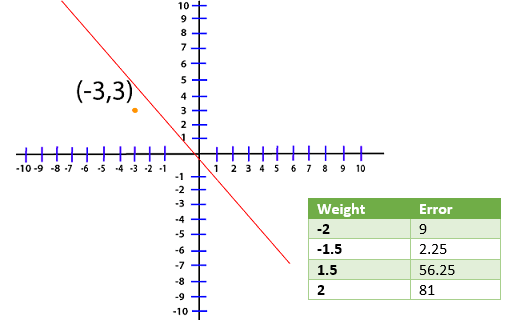
Now, whatever line that we are dealing with the optimal line will have a weight that will reduce this error as close to zero as possible. Now, we are dealing with the point (-3, 3) and for this loss, the function will translate to

Loss=(3-A(-3))2
Loss=(3+3A)2

Now, we create a table and try out the different value of A and see which one gives us the smallest error

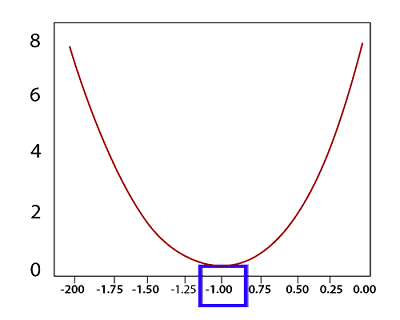
We have plot different error values for different weight in my plot level for visualization purpose.

The absolute minimum, in this case, corresponds to the weight of negative one now, that we know how to evaluate the error corresponding to our linear equation.

How do we train a model to know that this weight right here? For this, we use Gradient Descent.