Gradient Descent in PyTorch

Our biggest question is, how we train a model to determine the weight parameters which will minimize our error function. Let starts how gradient descent help us to train our model.

First, the linear model will begin with a random initial parameter recall when we initialize the model with the linear function. It indeed gave us a random initial parameter.

Let's ignore the bias value for now and based on the error associated with this initial parameter A. Our motive is to move in the direction that gives us the smaller error.

If we take the gradient of error function the derivatives of the slope of the tangent at the current value that we met, this derivative will take us in the direction of the highest error.

Loss=(3+3A)2
f' (A)=18(A+1)

So, we move it the negative direction of the gradient, which will take us in the direction of the lowest error. We take current to weight, and we subtract the derivatives of that function at that same point.

It will take us in the direction of the least error.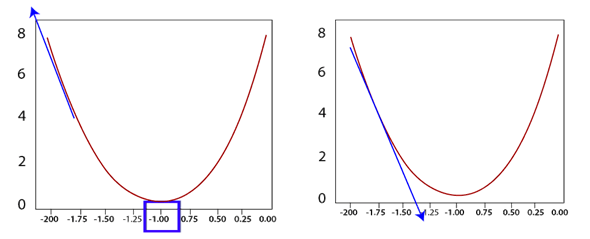

In a summarized way, first, we have to compute the derivatives of the loss function and then submission in the current weight value of the line. Whatever the weight maybe, they will give you the gradient value. This gradient value is then subtracted from the current weight A0, to give the new updated weight A1. The new weight should result in a smaller error than the previous one. We will do that iteratively until we obtain the optimal parameter for our line model to fit the data.

We are descending with the gradient, however, to ensure optimal results. One should descend in minimal steps. As such, we will multiply the gradient by a minimal number known as the learning rate. The value of the learning rate is empirical. Although a good standard starting value tends to be one over 10 or 1 over 100, the learning rate needs to be sufficiently small since as the line adjusting itself you never wanted to move drastically in one direction as that can cause for unwanted divergent behavior.

In this, we will learn to adjust the earning rate based on empirical results, and we will code a gradient descent algorithm later but follow through with our gradient descent example let's refer to a demonstration on excel to visualize the effect of gradient descent.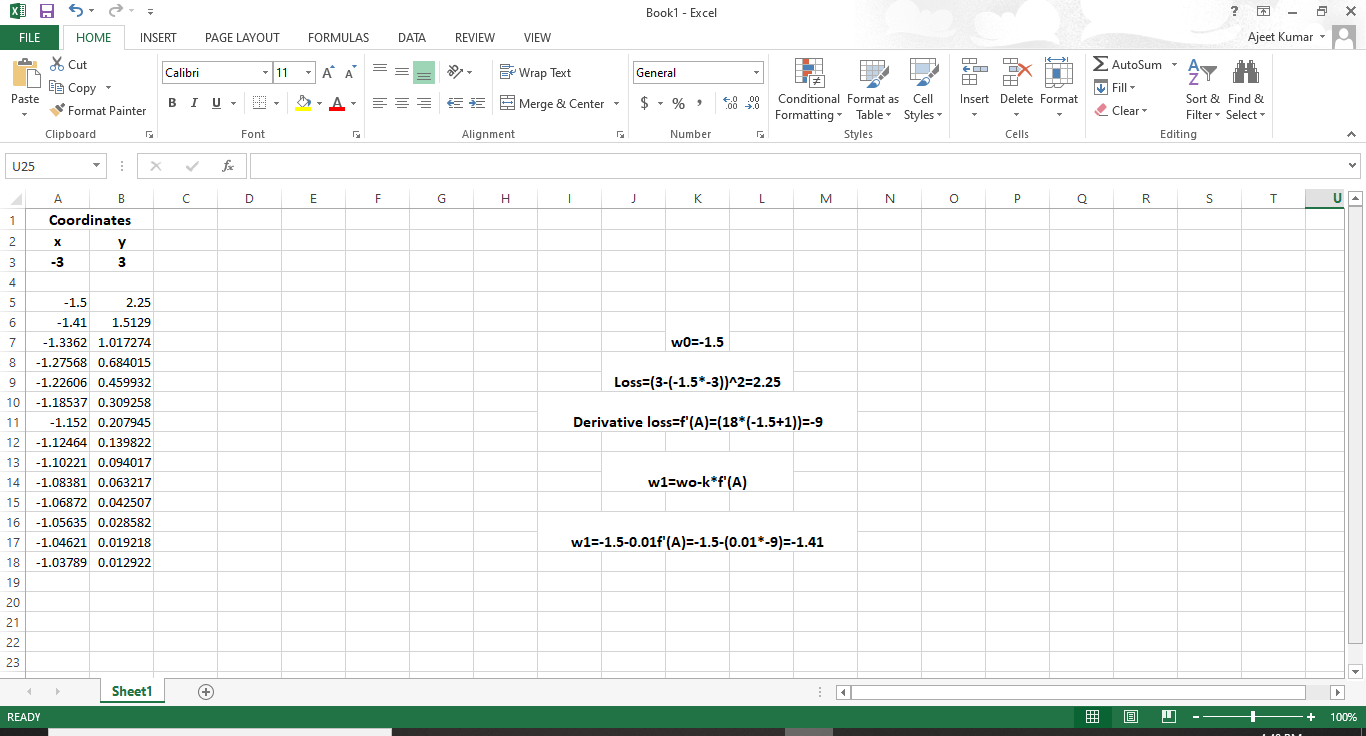

We will implement it later in our code.