Aptitude Decimal Fraction Concepts and Formulas
Points to Remember:
1. Decimal Fraction: An integer number which is separated by a decimal point is known as a decimal fraction.
For example, the number 0.1, 0.07, 0.00011, etc., are in decimal fractions.
If we convert the number into a vulgar fraction, the number's denominator will contain 10 or multiple of 10. For example, the number 0.1 = 1/10 and 0.55 = 55/100
2. Decimal Places: The number of figures which follow the decimal point is called the number of decimal places. Thus, 3.625 can be written as 3625/1000 that means we have three decimal places, and 5.39 have two decimal places.
3. Converting a decimal into a vulgar fraction: Write down the given number without the decimal point for the numerator, and for the denominator write 1 followed by as many zeros as many are the figures after the decimal point. For example, 3.423 = 3423/1000.
- Adding zeros to the extreme right of a decimal fraction does not change its value.
For example, 0.4 = 0.40=0.400=0.4000000
- If numerator and denominator have the same number of decimal place, we can remove the decimal sign.
For example, 0.72/0.18 is equal to 72/18.
- If numerator and denominator have the different number of decimal place, we have to equate both numbers of figures in decimal part by putting zeros, and then remove the decimals.
For example, 10/ 2.5 = 100/25 = 4
4. Adding and subtraction of decimals: Write down the numbers, placing the decimal points in one column. The numbers can now be added or subtracted in the usual way.
- For example: 13.725 + 6.275 = 20.000 = 20
- Subtraction: 13.72 - 3.225 is equals to 13.720 - 3.225 = 10.495
5. Multiplication of decimals:
- To multiply by 10, 100, 1000, etc., Move the decimal points by as many places to right as many are the zeros in the multiplier.
For example, 12.5*10 =125
- To multiply by a whole number: Multiply the number as in case of integers and place the decimal point in the product as many decimal places as in the multiplicand, prefixing zeros, if necessary.
For example, 12.5*7
Multiplicand = 12.5
Multiplier = 7
Now step 1: multiply by taking both of them as the integer value
125*7 = 875
Step 2: place the decimal in the product as many decimal places as in the multiplicand.
ATQ, the multiplicand has 1 decimal place.
So, the product will be 87.5 (decimal point after 1 decimal place).
- To multiply a decimal by a decimal: multiply as in integer, and place the decimal in product value as many decimal places as there are in the case of the multiplier and the multiplicand together, prefixing zeros, if necessary.
For example, 12.5*7.325
Multiplicand = 12.5
Multiplier = 7.325
Now step 1: multiply by taking both of them as the integer value
125*7325 = 915625
Step 2: place the decimal point in the product as many decimal places as there are in the case of the multiplier and the multiplicand together.
ATQ, multiplicand has 1 decimal place, and multiplier has three decimal places.
That means the Product will contain the decimal point after 1+3 = 4 decimal places.
So, the product of 12.5 * 7.325 = 91.5625
6. Division of decimals:
- When the divisor is 10, 100, 1000, etc., To divide a decimal by 10, 100, 1000, etc., move the decimal point 1, 2, 3, etc., places to the left respectively.
For example, 12.23/10 = 1.223 and 153.56/1000 = 0.15356
- When the divisor is a decimal fraction: Move the decimal point as many places to the right in the divisor to make the divisor as a whole number, annexing zeros to the dividend as many places as you moved the point to the right in the divisor.
For example, 125/5.5
Annexing zeros in the dividend to make the divisor as a whole number.
1250/55 = 22.7272......
7. Recurring Decimals: A decimal in which a figure or set of figures is repeated continually is called a recurring or periodic or circulating decimal. The repeated figures are a set of figures which is called the period of a decimal.
- Pure recurring decimal: A decimal number, in which all the digits after the decimal points are repeated, is called a pure recurring decimal.
For example, 2.3̅2̅1 is a pure recurring decimal because all the numbers after the decimal point are repeated.
- Mixed recurring decimal: A decimal number in which some digits do not recur after the decimal point, is called a mixed recurring decimal. For example, 0.5429 is a mixed recurring decimal because out of 542̅9 only 2 and 9 are recurring.
8. To convert a recurring decimal fraction into a vulgar fraction:
- Pure recurring decimal to vulgar fraction: A pure recurring decimal can be written as the vulgar fraction by putting as many nines as there are recurring digits after the decimal point, in the denominator of the vulgar fraction.
For example, 0.3̅2̅1= 321/999 and 3.2̅5 = 3+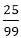
- Mixed recurring decimal to vulgar fraction: A mixed recurring decimal can be written as a vulgar fraction in which the numerator will contain the difference between the number formed by all the digits (after decimal point) and the numbers that do not recur; and the denominator will contain as many nines as there recurring digits, following by as many zeros as there are non-recurring digits.
For example, the number 0.32145 can be expressed as [32145- 321]/ 99000
9. Addition and subtraction of recurring decimals:
- Pure recurring decimal: First we have to convert the recurring decimal into an integer and then perform the addition or subtraction.
For example, the number 13.2̅4+ 15.2̅7 will add in two parts.
- Add the integer value that is on the left-hand side of the decimal point
Or, 13+15 = 28
- Now add the recurring value that is on the right-hand side of the decimal point
Or, 24+27 = 51
Hence, the addition of 13.2̅4+ 15.2̅7 = 28.5̅1
10. Mixed recurring decimal: addition and subtraction of mixed recurring decimals can be done in the following steps:
- Separate the expansion of recurring decimals into three parts. In the left-side part, there is an integer value with non-recurring decimal digits. In case of only one number contains the non-recurring value then the other one who has only recurring value will place his recurring value to make the same decimal place in both numbers.
- In the middle part, we have to count that how many recurring values are in the first number and the second number, and then take the LCM of both. Repeat the recurring number LCM's number of times in the middle part.
I- n the last part, it doesn't matter that how many recurring digits are there in the numbers, we have to put two recurring digits always in the third-part.
For example,
Let there are two numbers a = 3.7̅6, b = 1.45̅7̅6
We have to find a+b and a-b.
Here, the number "a" has 2 recurring numbers, and the number "b" contains 3 recurring numbers and 1 non-recurring number.
LCM of recurring digits (2, 3) = 6, that means middle part will contain repetition of recurring digits 6 times.
Now, separate the expression in 3 parts.
| 3.7(left-hand side value, and one recurring value (because a has no any non-recurring value) to make the decimal place equal in both numbers) |
676767 (recurring value starts from 6 because recurring digit 7 already used in the left-side part) |
67 (repeat only two digits of recurring value always) |
| 1.4 (left-hand side value, and non-recurring value) |
576576 |
57(repeat only two digits of recurring value always) |
| Addition= 5.2 |
676767+576576 = 253344 |
24(the value of third-part is not taken into consideration while final answer) |
Hence, the addition of 3.7̅6 + 1.45̅7̅6 = 5.22̅5̅3̅3̅4̅4
Similarly subtraction can be done.
11. Multiplication of Recurring Decimals:
- While multiplying a recurring decimal by a multiple of 10, the set of repeating digits is not altered.
For example, let the multiplicand = 3.5̅7, and multiplier = 10
Now, 3.5̅7 can be written as 3.575757.... * 10 = 35.7575757.....
We know that the repeating value will not be altering so the recurring number will be the same. i.e., 35.75̅7̅5̅7̅5̅7
- While multiplying a recurring decimal by a number which is not a multiple of 10, first all of the recurring decimal is changed into a vulgar fraction, and then the calculation is done.
For example, let the multiplicand = 7.6̅3̅, and multiplier = 11
Now, 7.6̅3 can be written as 7+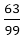 * 11 * 11
Or, (7 +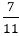 )*11 = 11*7 +7 = 84 )*11 = 11*7 +7 = 84
So, the result will be 84
12. Approximation and contraction: increase the figure after the decimal point to the nearest 10 if the succeeding figure is 5 or greater than 5.
For example, the approximate value of 10.68 is 10.7
13. HCF and LCM of decimal fractions: the HCF and the LCM of a decimal number can found in two steps:
- First, you have two make the number of digit (value after decimal) equal in the decimal numbers by adding zeros in the suffix if necessary.
- Now assume that both the numbers are an integer and then get the HCF and LCM of that number. Place the decimal point in the result as many decimal places as in the in the initial number.
For example, 0.36 and 1.08
Now, express each of the numbers without the decimals as the product of primes and we get:
36 = 2 × 2 × 3 × 3 = 22 × 32
108 = 2 × 2 × 3 × 3 × 3 = 22 × 33
Now, H.C.F. of 36 and 108 = 22 × 32 = 36
Therefore, the H.C.F. of 0.36 and 1.08 = 0.36 (taking 2 decimal places)
L.C.M. of 36 and 108 = 22 × 33 = 108
Therefore, L.C.M. of 0.36 and 1.08 = 1.08 (taking 2 decimal places)
14. Comparison of fractions: convert each one of the given fractions in the decimal form. Now, arrange them in the required order.
For example, 3/10, 10/7, 5/9
Convert them in decimal form:
3/10= 0.3
10/7 = 1.428
5/9 = 0.555...
Now compare each and arrange in ascending or descending order.
Ascending order: 0.3<0.555<1.428
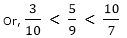
Aptitude Decimal Fraction Test Paper 1
Aptitude Decimal Fraction Test Paper 2
Aptitude Decimal Fraction Test Paper 3
Aptitude Decimal Fraction Test Paper 4
Aptitude Decimal Fraction Test Paper 5
|
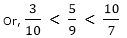
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now




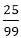
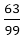 * 11
* 11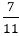 )*11 = 11*7 +7 = 84
)*11 = 11*7 +7 = 84




