Aptitude Height and Distance Test Paper 11) Two ships are sailing in the sea on the two sides of a lighthouse. The angles of elevation of the top of the lighthouse observed from the ships are 30° and 45° respectively. If the lighthouse is 100m high, find the distance between the two ships.
The Correctoption is(B) Answer with explanation: 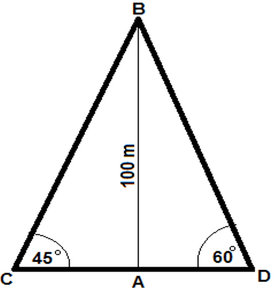
Let AB be the height of lighthouse and C and D be the positions of the ships. AB = 100 meters, ∠ACB = 45°, ∠ADB = 60° 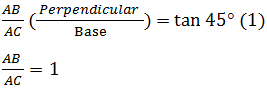
AC = AB (100m) AC = 100 m 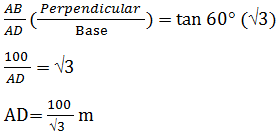
Distance between ships, CD = AC + AD 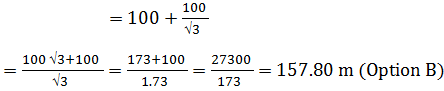
2) A ladder is leaning against a wall. It makes a 60° angle with the wall. If the distance between foot of ladder and wall is 5.5 meters, find the length of the ladder.
The Correctoption is(D) Answer with explanation: 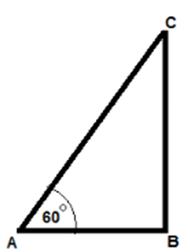
Let BC be the wall and AC be the ladder. ∠BAC = 60° and AB = 5.5 meter 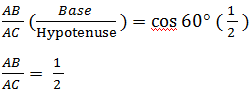
AC = 2 * AB = 2 * 5.5 = 11 meters (Option D) 3) A man 1.5 meter tall is 30√3 meter away from a building. When he sees the top of building the angle of elevation is 30°. Find the height of the building?
The Correctoption is(A) Answer with explanation: 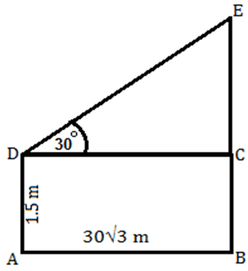
Let AD be the man and BE the building. Now draw a line DC so that DC is perpendicular to BE. Now, BC = AD = 1.5 m And, DC = AB = 30√3 m 
Now, Height of building, BE = BC + EC = 1.5 + 30 = 31.5 m (Option A) 4) The angle of elevation of the top of a tower at a point X is 30°. On walking 30 m towards the tower if the angle of elevation becomes 60° at point Y, find the height of the tower?
The Correctoption is(A) Answer with explanation: 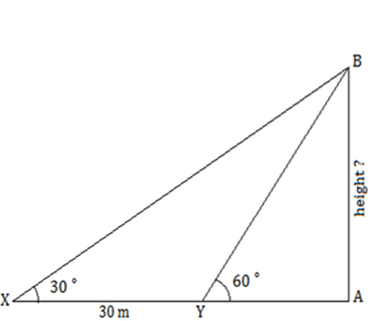
Let AB be the height of tower and XA be the distance between point X and base of tower. 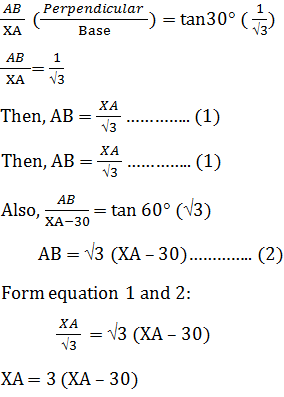
XA = 3XA - 90 - 2XA = - 90 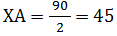
Put the value of XA in equation (1) to find AB (height of tower). 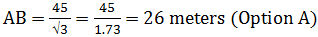
5) The tops of two poles are connected by a wire. The heights of the poles are 10 m and 14 m respectively. If the wire makes a 30° angle with the horizontal, find the length of the wire?
The Correctoption is(C) Answer with explanation: 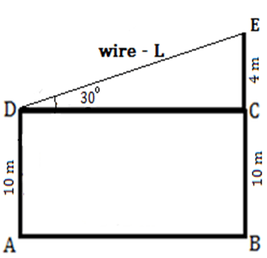
Let AD and BE, be the poles of height 10 m and 14 m respectively. DE is the wire of length = L DC is parallel to AB so AD = BC = 10 m So, CE = BE - BC = 14 - 10 = 4 m 
Height and Distance Aptitude Test Paper 2
Height and Distance Aptitude Test Paper 3 Height and Distance Aptitude Test Paper 4 |
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share









