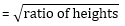Aptitude Volume and Surface Area Concepts and formulas1) Cuboid: Let length = l, breadth = b, and height = h units
2) Cube: Let each edge of a cube = "a" units. Then:
3) Cylinder: Let the radius of the base of a cylinder be r units and height of the cylinder be h units. Then:
4) Sphere: Let r be the radius of the sphere. Then:
5) Right circular cone: Let r be the radius of the base, h is the height, and l is the slant height of the cone. Then:
6) Frustum of a right circular cone: Let the radius of the base of the frustum = R, the radius of top = r, height = h and slant height = l units.
Some Quicker methods:1) For a closed wooden box:
2) Problems involving ratios: I. Two Spheres: (i) (Ratio of radii)2 = ratio of surface areas. (ii) Ratio of volumes = (ratio of radii)3 (iii) (Ratio of surface areas)3 = (ratio of volumes)2 II. Two cylinders: a. When the radii are equal: (i) Ratio of volumes = ratio of heights. (ii) Ratio of curved surface areas = ratio of heights (iii) Ratio of volumes = (ratio of curved surface areas) b. When heights are equal (i) Ratio of volumes = (ratio of radii)2 (ii) Ratio of curved surface areas = ratio of radii (iii) Ratio of volumes = (ratio of curved surface areas)2 c. When volumes are equal (i) Ratio of radii (ii) Ratio of curved surface areas d. When curved surface areas are equal (i) Ratio of volumes = ratio of radii (ii) Ratio of volumes = inverse ratio of heights. (iii) Ratio of radii = inverse ratio of heights. Aptitude Volume and Surface Area Test Paper 1 Aptitude Volume and Surface Area Test Paper 2 Aptitude Volume and Surface Area Test Paper 3 Aptitude Volume and Surface Area Test Paper 4 Aptitude Volume and Surface Area Test Paper 5 |
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share




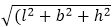 units.
units. 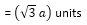
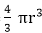 cubic units.
cubic units.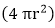 sq. units.
sq. units.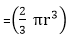 cubic units.
cubic units.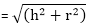
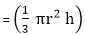 cubic units.
cubic units.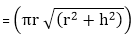 sq. units.
sq. units.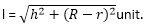
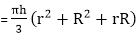 cubic units.
cubic units.