Aptitude H.C.F and L.C.M Concepts and Formulas

Points to remember:

1. Factor: Factor of a number is a number which divides the number evenly. For example, 15 can be divided evenly by 1, 3, 5, and 15 so the factors of 15 are 1, 3, 5 and 15.

2. Common Factor: A common factor is a number which divides the two or more numbers exactly or evenly.

3. Highest Common Factor (H.C.F): HCF of the two numbers is the highest number of the two numbers which divides them exactly.

4. Methods to find the H.C.F of two or more numbers:

1. Method of prime factors: Break the given numbers into prime factors and then find the product of all prime factors common to all the numbers. The product will be the required HCF.
2. Method of Division: Divide the greater number by smaller number, divide the divisor by the remainder, and divide the remainder by the next remainder, and so on until no number is left. The last divisor is the required HCF.
3. To find the HCF of more than two numbers: Firstly find the HCF of first two numbers and then find the HCF of this HCF and the third number and so on and the last HCF will be the required HCF.
4. HCF of decimals: Firstly, make the same number of decimal places in all the given numbers and then find the HCF of the numbers as if they are integers and mark the decimal places as there in each of the numbers.
5. HCF of the vulgar fraction: HCF of two or more fraction is the highest fraction which is exactly divisible by each of the fractions.

5. Common Multiple: Common multiple is the common number between two or more numbers which is exactly divisible by each number.

6. Least Common Multiple (LCM): LCM is the smallest number between the two numbers which exactly divides both of them.

7. Methods to find the LCM of two or more given numbers:

1. Method of Prime Factors: Resolve the given numbers into their prime factors and then find the product of the highest power of all the factors that occur in the given numbers. This product is the LCM.
2. The LCM of several small numbers can be easily found by the following rule:
   Write down the given numbers in a line separating them by commas. Divide them by any one of the prime number 2, 3, 5, 7, etc., which exactly divides at least any two of the given numbers. Write down the quotient and the undivided numbers in a line below the first. Repeat the process to get a line of numbers which are Prime to one another. The product of all divisors and the numbers in the last line will be the required LCM.
3. LCM of decimals: First make the same number of decimal places in all the given numbers. Then find their LCM and mark in the result as many decimal places as there are in each of the numbers.
4. LCM of fractions: The LCM of two or more fractions is the least fraction or integer which is exactly divisible by each of them.
   Express the fractions in their lowest terms, then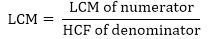

8. HCF x LCM = 1^st number x 2^nd number