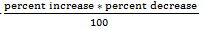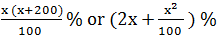Percentage Concepts and FormulasPoints to remember:1) The term percent comes from the Latin phrase 'per centum' which means per hundred or for every hundred. It is a fraction whose denominator is 100 and numerator is percent, e.g. 40% or 2) How to convert a fraction into a percent: To convert a fraction into percent multiply it by 100, e.g. 3) How to convert a percent into a fraction: Divide the number by 100 and drop the percent symbol, e.g. 60% 4) The percentage of a given number 'n' is given by; x % of a given number 'n' = E.g. 70% of 200 = Some quicker methods:1) If two values are respectively x% and y% more than a third value, the first value is And, the second value is 2) If two values are respectively x% and y% less than a third value, the first value is And, the second value is 3) If the price of a commodity increases by x %, the reduction in consumption so as not to increase the expenditure is given by; 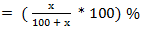
If the price of a commodity decreases by x %, the increase in consumption so as not to decrease the expenditure is given by; 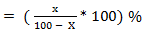
4) If A is x% of C and B is y% of C, A would be 5) Percentage fraction table: Some important fractions to remember 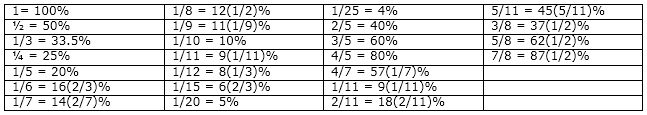
5) x % of a quantity is taken by A, y % of the remaining is taken by B and z % of the remaining is taken by C. If P is left in the fund, there was 6) x % of a quantity is added, y% of the increased quantity is added, again z % of the increased quantity is added and it becomes A, the initial amount is given by;
7) The population of a town is P. If it increases by x % in the first year, y % in the second year and z% in the third year, the final population after three years is given by;
And, if the population decreases by y % in the second year, the population after three years is given by;
Similarly, if the present population of a city changes (increases or decreases) at r % per annum, the population after n years is given by; 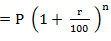
And, the population n years ago is given by; 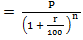
Note: Use '+' sigh if the population is increasing at r % per annum and use '-' sign if it is decreasing at r % per annum. 8) If a number is r % more than the second number, the second number will be 9) If a number is r % less than the second number, the second number will be 10) If a value is increased by x % and later decreased by x %, net change in the value is always a decrease which is equal to x % of x or 11) If a value is first increased by x %, decreased by y%, there will be 12) If a value is increased by x % and y % successively, the final increase in the value is given by; 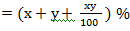
13) If the price of a product is reduced by x % and its consumption is increased by y % or the price is increased by x % and consumption is decreased by y%, the effect on revenue is given by; = percent increase - percent decrease = '+' sign will show an increase and '-' sign will show a decrease in the value. 14) The pass marks in an examination are x %. If a student secures y marks and fails by z marks, the maximum marks are given by; 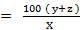
15) A candidate scores x % marks in an examination and fails by 'a' marks. If another candidate who scores y % marks which is 'b' marks more than the required pass marks, the maximum marks for this examination are given by; 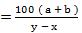
16) The sides of a triangle are measured. If one side is taken x % in excess and the other side is taken y% in deficit, the error percent in area calculated from these measurements is given by; 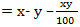
'+' sign will show the excess and '-' sign will show the deficit in the area. 17) If the sides of a triangle, rectangle, square or any other two-dimensional shape are increased by x %, the area is increased by 18) In an examination, x% students failed in one subject and y% students failed in another subject. If z% students failed in both the subjects, the percentage of students who passed in both the subjects is given by; = 100 - (x + y - z) Percentage Aptitude Test Paper 1 Percentage Aptitude Test Paper 2 Percentage Aptitude Test Paper 3 Percentage Aptitude Test Paper 4 Percentage Aptitude Test Paper 5 Percentage Aptitude Test Paper 6 Percentage Aptitude Test Paper 7 Percentage Aptitude Test Paper 8
Next TopicAptitude Percentage Test Paper 1
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share




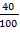 . In mathematics, percent is denoted by the symbol '%'.
. In mathematics, percent is denoted by the symbol '%'.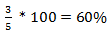
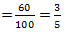
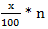
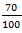 * 200 = 140
* 200 = 140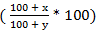 % of the second value.
% of the second value.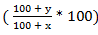 % of the first value.
% of the first value.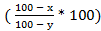 % of the second value.
% of the second value.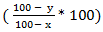 % of the first value.
% of the first value.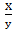 * 100 % of B.
* 100 % of B.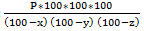 in the beginning.
in the beginning.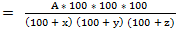
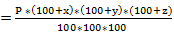
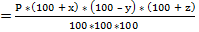
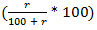 % less than the first number, e.g. If A's income is r % more than B's income, B's income is
% less than the first number, e.g. If A's income is r % more than B's income, B's income is 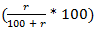 % less than A's income.
% less than A's income.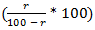 % more than the first number.
% more than the first number.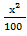 .
.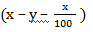 % increase or decrease in the value, i.e. '+' sign will show an increase and '- 'sign will show a decrease in the value.
% increase or decrease in the value, i.e. '+' sign will show an increase and '- 'sign will show a decrease in the value.