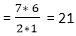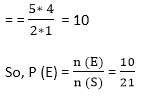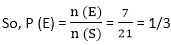Probability Aptitude Test Paper 11) What is the probability of getting an even number when a dice is rolled?
Answer: B Explanation: The sample space when a dice is rolled, S = (1, 2, 3, 4, 5 and 6) 2) What is the probability of getting two tails when two coins are tossed?
Answer: D Explanation: The sample space when two coins are tossed = (H, H), (H, T), (T, H), (T, T) 3) The tickets numbered from 1 to 20 are mixed up and then a ticket is drawn at random. What is the probability that the ticket has a number which is a multiple of 3 or 5?
Answer: A Explanation: The sample space, S= (1, 2, 3, 4, 5 ...18, 19, 20) or n(S) = 20 The event "E" of getting a multiple of 3 or 5 = (3, 6, 9, 12, 15, 18, 5, 10, 20) or n (E) = 9 4) A box contains 2 red, 3 green, and 2 blue balls. What is the probability that none of the balls drawn is blue?
Answer: B Explanation: Total number of balls = (2+3+2) = 7 Let E is the event of drawing 2 balls, none of which is blue. n (E) = number of ways of drawing 2 balls out of (2+3) balls. = 5C2
5) In a bag, there are 8 red, 7 yellow and 6 green balls. If one ball is picked up at random, what is the probability that it is neither red nor green?
Answer: D Explanation: Total number of balls or sample space = 8 + 7+ 6 = 21 Probability Aptitude Test Paper 2 Probability Aptitude Test Paper 3
Next TopicProbability Aptitude Test Paper 2
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share




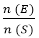 = 3/6 = 1/2
= 3/6 = 1/2