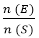Aptitude Probability Concepts and Formulas

Points to Remember:

1) Probability: It is the quantitative measure of the chance of occurrence of a particular event. It tells about the chance or likelihood of the occurrence of a particular event. It can be expressed as proportions that range from 0 to 1, or can also be expressed as percentages that range from 0% to 100%. For example, a probability of 40 % (0.40) indicates that there are 40 chances out of 100 of the occurrence of an event.

2) Experiment: It is an operation that can be infinitely repeated and has well-defined set of possible outcomes, which is known as a sample space. Each outcome is known as an event. For example, tossing a coin is an experiment that produces two well-defined outcomes: Head and Tail.

3) Random Experiment: It refers to an experiment whose possible outcomes are known but the exact outcome cannot be predicted in advance. For example:

i) Tossing of a coin:

When we toss a coin, the outcome will be either (H) or Tail (T)

ii) Throwing a dice:

A dice has six faces, each with a different number of dots from one to six. When a dice is thrown, any number from one to six can appear on its upper face. So the outcome can be 1 or 2 or 3 or 4 or 5 or 6.

iii) Drawing a card from a pack of 52 playing cards:

A pack of playing cards has 52 cards which are divided into four categories which are as follows:

• Spades
• Clubs
• Hearts
• Diamonds

Each category has 13 cards out of which nine cards are numbered from 2 to 10; remaining cards include an Ace, a King, a Queen, and a Jack.

The hearts and diamonds are red in colour, whereas spades and clubs are black in colour. Furthermore, kings, queens, and jacks are called face cards.

iv) Taking a ball randomly from a bag that contains balls of different colours.

4) Sample Space: It refers to the all possible outcomes of an experiment. It is denoted by S.

For example:

When a coin is tossed, the possible outcomes include Head and Tail. So, S in this case, = (H, T)

When two coins are tossed, there are four possible outcomes, i.e. S= (HH, HT, TH, TT)

When a dice is thrown, there are six possible outcomes, i.e. S = (1, 2, 3, 4, 5, and 6)

5) Event: It refers to a subset of a Sample Space. It is generally denoted by a capital letter "E". For example:

a. When a coin is tossed, the outcome head or tail is called an event. Total number of events in this case, n (E) =2 (head and tail).

b. When a dice is rolled, the outcome 1 or 2 or 3 or 4 or 5 or 6 is an event. Total number of events in this case, n (E) =6 (1 to 6).

6) Probability of an Event

Let E be an event and S is the sample space. Then the probability of the event E is given by:

P (E) =

P (E) = Probability of an Event

n (E) = number of ways in which an event can occur

n (S)= Total number of possible outcomes

Example: Let us find out the probability of getting Head when a coin is tossed once.

Total number of possible outcomes = n (S) = 2 (head or tail)

Total number of ways in which the event can occur = n (H) = 1

So, P (E) = n (E)/n(S) = 1/2 or 50%

7) Equally Likely Events: The events in which there is no preference for a particular event over the other are known as equally likely events.

Examples:

I) When a coin is tossed, the head and tail are equally likely events.

II) When a dice is thrown, all the six outcomes (1, 2, 3, 4, 5, and 6) are equally likely to occur, so they are equally likely events.

8) Mutually Exclusive Events: The two or more events in which the occurrence of one of the events excludes the occurrence of the other event are known as the mutually exclusive events.

For example:

i) When a coin is tossed, the outcome is head or tail. Head and tail cannot appear simultaneously. So, in this case, the occurrence of Head and Tail are mutually exclusive events.

ii) When a dice is rolled, all the numbers cannot appear simultaneously, so they are mutually exclusive events.

iii) Let a dice is thrown and A be the event of getting 2 or 4 or 6 and B be the event of getting 4 or 5 or 6. Then

A = (2, 4, 6) and B = (4, 5, 6)

So, A and B are not mutually exclusive events, as 4 and 6 are present in both the events.

9) Independent Events: The events in which the occurrence or non-occurrence of one event does not influence the occurrence or non-occurrence of the other event.

For example: When a coin is tossed twice, the event of getting Head (H) in the first toss and the event of getting Head (H) in the second toss are independent events. This is due to the fact that the occurrence of getting Head (H) in the first toss does not influence the occurrence of getting Head (H) in the second toss.

10) Simple Events: It refers to the events where one experiment happens at a time and it has a single outcome. The probability of simple events is denoted by P (E) where E is the event. In the case of simple events, we consider the probability of occurrence of single events. For example:

i) Probability of getting a tail (T) when a coin is tossed.

ii) Probability of getting 6 when a dice is thrown.

11) Compound Event: It refers to an event in which there is more than one possible outcome. In other words, the event in which we take the probability of the joint occurrence of two or more events is known as a compound event. For example:

i) When two coins are tossed, the probability of joint occurrence of Head (H) in the one coin and Tail (T) in another coin is a compound event.

12) Exhaustive Events: The mutually exclusive events that form the sample space collectively are called the exhaustive events. For example, when a coin is tossed, either Head or Tail appears and they collectively form the sample space. So, there are two exhaustive events.

13) Algebra of Events

Let A and B are two events and S is the sample space when a dice is thrown. Then

Let A = (2, 4, 6) and B = (4, 5, 6), then:

i) A ∪ B is the event in which either A or B or both A and B occur. For example, A ∪ B = (2, 4, 5, 6)

ii) A ∩ B is the event in which both A and B occurs. For example, A ∩ B = (4, 6)

iii) A̅ is the event in which A does not occur. For example, A̅ = (1, 3, 5)

iv) B̅ is the event in which B does not occur. For example, B̅ = (1, 2, 3)

iv) A̅ ∩B̅ is the event in which none of A and B occurs. A̅ ∩B̅ = (1, 3)

14) Additional Theorem

Let A and B are two events associated with a random experiment. Then

P (A U B) = P (A) + P (B) - P (A∩B), if P (A∩B) ≠ 0

If A, and B are mutually exclusive events, P (A U B) = P (A) + P (B) as P (A∩B) = 0 for mutually exclusive events.