Aptitude Height and Distance Test Paper 416) The top and bottom of a flag on a building subtend angles of 60° and 30° respectively at a point B which is 48 meter away from the building. Find the height of the flag?
The Correctoption is(B) Answer with explanation: 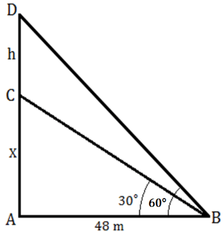
Let height of building be AC = X and height of flag be CD = h. 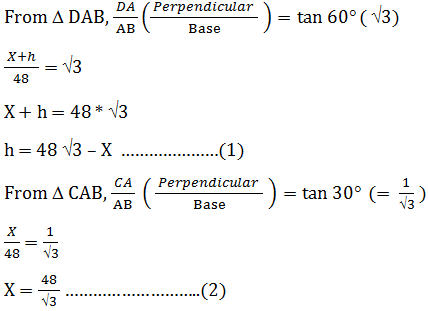
Put value of X in equation (1) from equation (2) 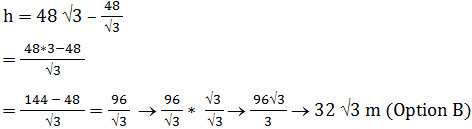
17) From the top of a lighthouse which is 90 m above the sea, the angle of depression of a ship is 60°. How far is the ship from the lighthouse?
The Correctoption is(A) Answer with explanation: 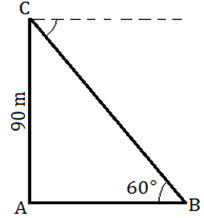
Let the height of the lighthouse above sea be AC and it is given 90 m. Ship is at point B so the distance between the base of lighthouse A and ship is AB. 
18) The angles of elevation of the top of a tower from the top and bottom of a tree of height 15 m are 30° and 60° respectively. Find the height of the tower?
The Correctoption is(B) Answer with explanation: 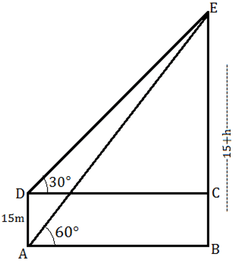
Let the CE be h meter. Height of tree be AD = 15m BE is the height of tower = BC + CE = 15 + h AB = CD, let it is = X m 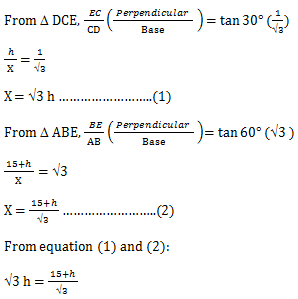
3 h = 15 + h 2 h = 15 h = 7.5 m Height of tower = 15 + 7.5 = 22.5 m (Option B) 19) The distance between the tops of two trees is 16 m. If the heights of the trees are 20 m and 28 m respectively, find the horizontal distance between the two trees?
The Correctoption is(B) Answer with explanation: 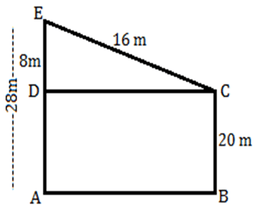
Let AE and BC be the heights of trees. AE = 28 m BC = 20 m Horizontal distance between trees AB = DC In Δ EDC, EC2 = ED2 + DC2 (Pythagoras theorem) DC2 = EC2 - ED2 = 162 - 82 = 256 - 64 DC2 = 192 DC =√192 m (Option B) 20) There are two towers. The first tower of height 60 m casts a shadow of length 100m. At the same time if the second tower casts a shadow of length 140 m, find its height?
The Correctoption is(B) Answer with explanation: 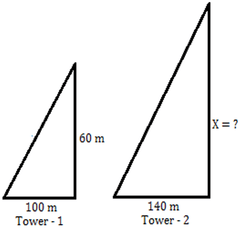
Let the height of the second tower = X We know that the length of the shadow is directly proportional to the height of the tower. 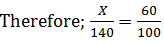
X = 84 m (Option B)
Height and Distance Aptitude Test Paper 2
Height and Distance Aptitude Test Paper 3 Height and Distance Aptitude Test Paper 1 |
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share









