Aptitude Logarithm Test Paper 416) If log10 x = a, log10 y = b, and log10 z = c, so (to base 10) the antilogarithm of pa+qb+rc would be
Answer: B Explanation: Let x = antilog (pa+qb+rc)z Or, we can say that log x = pa+qb+rcz Or, log x = p log10 x + q log10 y + r log10 z We know that, p log q = log qp Or, log x = log10 xp + log10 yq + log10 zr Or, we know that log a + log b = log ab Or, log x = log (xp yq zr) Since, both sides log will be canceled out Therefore, x = xp yq zr) Hence, the antilogarithm of pa+qb+rc = x xp yq zr) 17) The value of logb a2 logc b2 loga c2 is
Answer: C Explanation: We have an expression logb a2 logc b2 loga c2 Similarly, (2 logb a) (2 logc b) (2 loga c) Therefore, 8 * 1 = 8 18) If log(x2 - 4x + 5) = 0, what will be the value of x?
Answer: A Explanation: We have log(x2 - 4x + 5) = 0 Note: when log moves from one side to the other, it will become exponential. So, (x2 - 4x + 5) = e0 Or, we know that exponential to the power zero is one. So, x2 - 4x + 5 = 1 Now, x2 - 4x + 5-1 = 0 Or, x2 - 4x + 4 = 0 Or, (x-2) 2 = 0 Therefore, x- 2 = 0 Hence, x = 2 19) If log2 [log3 (log2 x)] = 1, what is the value of x?
Answer: A Explanation: We have an expression log2 [log3 (log2 x)] = 1 We know that, logx y = a, is equals to xa = y Similarly, [log3 (log2 x)] = 21 Now, log2 x = 32 = 9 Now, x = 29 = 512 Therefore, the value of x from the expression log2 [log3 (log2 x)] = 1, is 512. 20)
Answer: C Explanation: We know that log m + log n + log p = log (m * n * p) Now, we can write it as, log Note: logx (1) is always equals to be zero. Aptitude Logarithm Test Paper 1 Aptitude Logarithm Test Paper 2 Aptitude Logarithm Test Paper 3
Next TopicAptitude Logarithm Concepts
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share




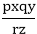
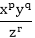
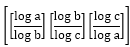
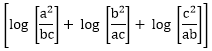 is equal to
is equal to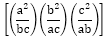
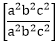 => log (1)
=> log (1)




