Rotation about Arbitrary Axis

When the object is rotated about an axis that is not parallel to any one of co-ordinate axis, i.e., x, y, z. Then additional transformations are required. First of all, alignment is needed, and then the object is being back to the original position. Following steps are required

1. Translate the object to the origin
2. Rotate object so that axis of object coincide with any of coordinate axis.
3. Perform rotation about co-ordinate axis with whom coinciding is done.
4. Apply inverse rotation to bring rotation back to the original position.


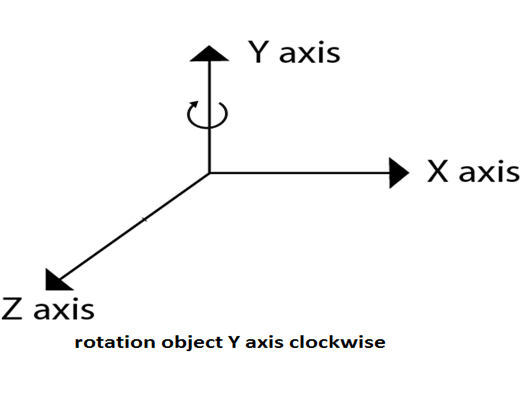
Matrix for representing three-dimensional rotations about the Z axis



Matrix for representing three-dimensional rotations about the X axis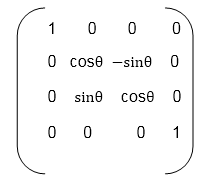



Matrix for representing three-dimensional rotations about the Y axis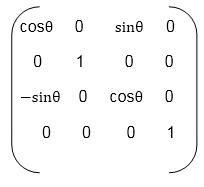



Following figure show the original position of object and position of object after rotation about the x-axis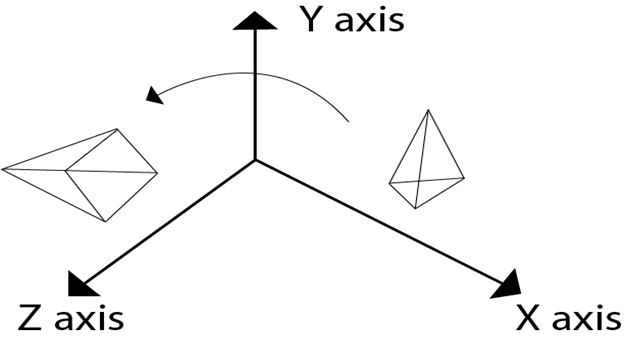



5. Apply inverse translation to bring rotation axis to the original position.

For such transformations, composite transformations are required. All the above steps are applied on points P' and P".Each step is explained using a separate figure.

Step1: Initial position of P' and P"is shown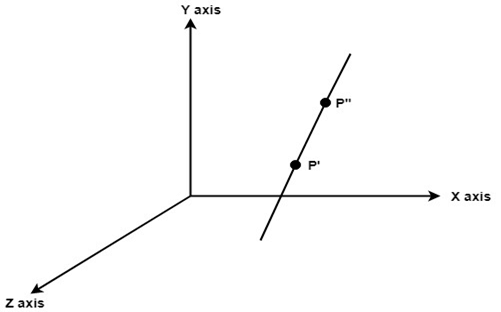



Step2: Translate object P' to origin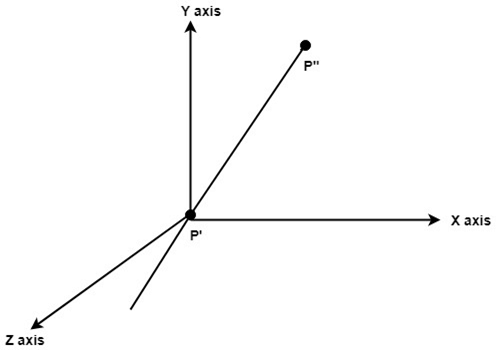



Step3: Rotate P" to z axis so that it aligns along the z-axis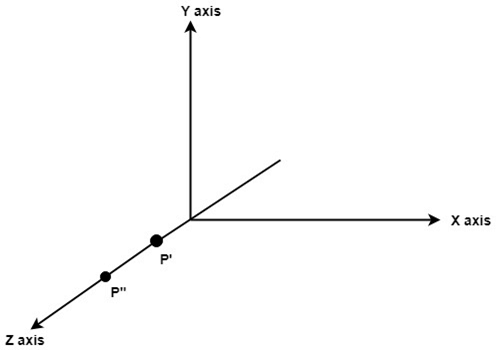



Step4: Rotate about around z- axis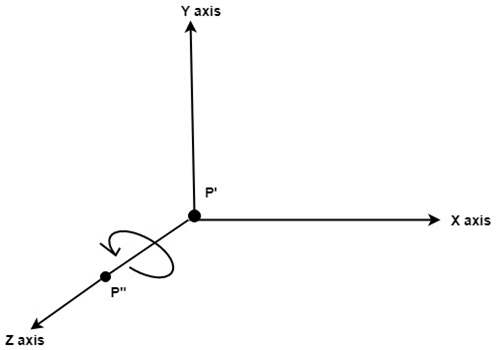



Step5: Rotate axis to the original position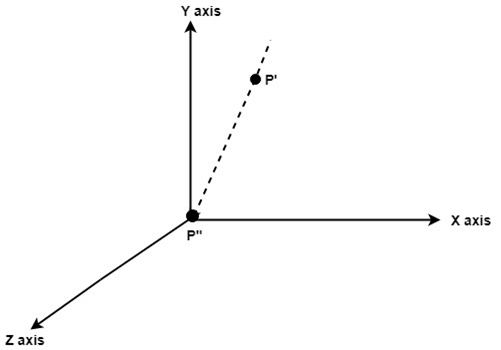



Step6: Translate axis to the original position.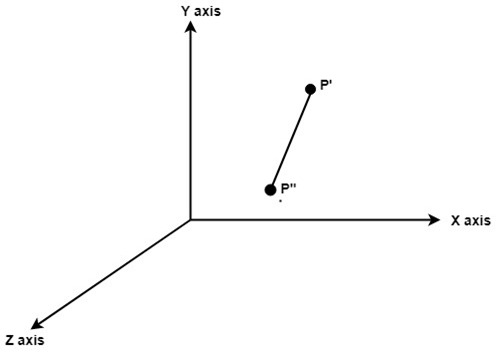



---

Next TopicInverse Transformations



← prev next →