Homogeneous CoordinatesThe rotation of a point, straight line or an entire image on the screen, about a point other than origin, is achieved by first moving the image until the point of rotation occupies the origin, then performing rotation, then finally moving the image to its original position. The moving of an image from one place to another in a straight line is called a translation. A translation may be done by adding or subtracting to each point, the amount, by which picture is required to be shifted. Translation of point by the change of coordinate cannot be combined with other transformation by using simple matrix application. Such a combination is essential if we wish to rotate an image about a point other than origin by translation, rotation again translation. To combine these three transformations into a single transformation, homogeneous coordinates are used. In homogeneous coordinate system, two-dimensional coordinate positions (x, y) are represented by triple-coordinates. Homogeneous coordinates are generally used in design and construction applications. Here we perform translations, rotations, scaling to fit the picture into proper position. Example of representing coordinates into a homogeneous coordinate system: For two-dimensional geometric transformation, we can choose homogeneous parameter h to any non-zero value. For our convenience take it as one. Each two-dimensional position is then represented with homogeneous coordinates (x, y, 1). Following are matrix for two-dimensional transformation in homogeneous coordinate: 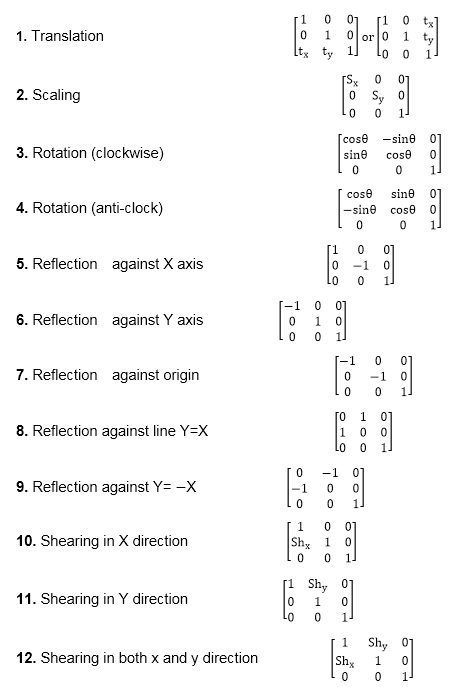
Next TopicComposite Transformation
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share










