Composite Transformation:A number of transformations or sequence of transformations can be combined into single one called as composition. The resulting matrix is called as composite matrix. The process of combining is called as concatenation. Suppose we want to perform rotation about an arbitrary point, then we can perform it by the sequence of three transformations
The ordering sequence of these numbers of transformations must not be changed. If a matrix is represented in column form, then the composite transformation is performed by multiplying matrix in order from right to left side. The output obtained from the previous matrix is multiplied with the new coming matrix. Example showing composite transformations:The enlargement is with respect to center. For this following sequence of transformations will be performed and all will be combined to a single one Step1: The object is kept at its position as in fig (a) Step2: The object is translated so that its center coincides with the origin as in fig (b) Step3: Scaling of an object by keeping the object at origin is done in fig (c) Step4: Again translation is done. This second translation is called a reverse translation. It will position the object at the origin location. Above transformation can be represented as TV.STV-1 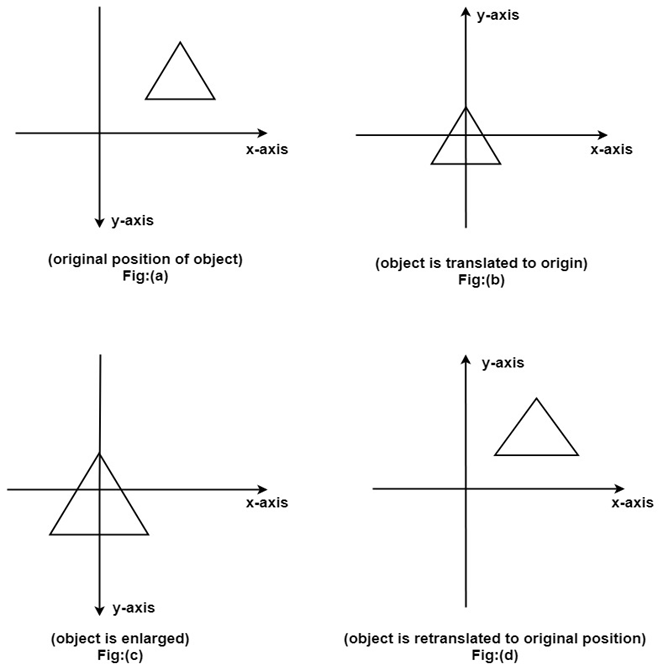
Note: Two types of rotations are used for representing matrices one is column method. Another is the row method.
Advantage of composition or concatenation of matrix:
Composition of two translations:Let t1 t2 t3 t4are translation vectors. They are two translations P1 and P2. The matrix of P1 and P2 given below. The P1 and P2are represented using Homogeneous matrices and P will be the final transformation matrix obtained after multiplication. 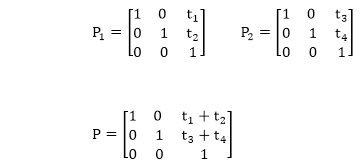
Above resultant matrix show that two successive translations are additive. Composition of two Rotations: Two Rotations are also additive Composition of two Scaling: The composition of two scaling is multiplicative. Let S11 and S12are matrix to be multiplied. 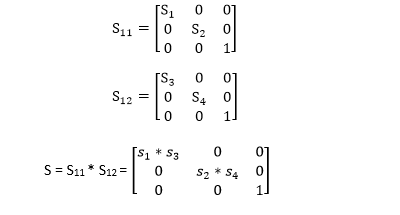
Next TopicPivot Point Rotation
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share










