Mid Point Subdivision Line Clipping Algorithm:It is used for clipping line. The line is divided in two parts. Mid points of line is obtained by dividing it in two short segments. Again division is done, by finding midpoint. This process is continued until line of visible and invisible category is obtained. Let (xi,yi) are midpoint 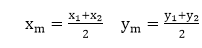 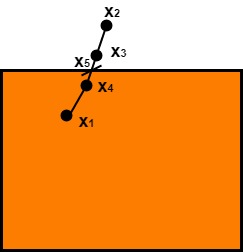 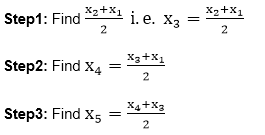
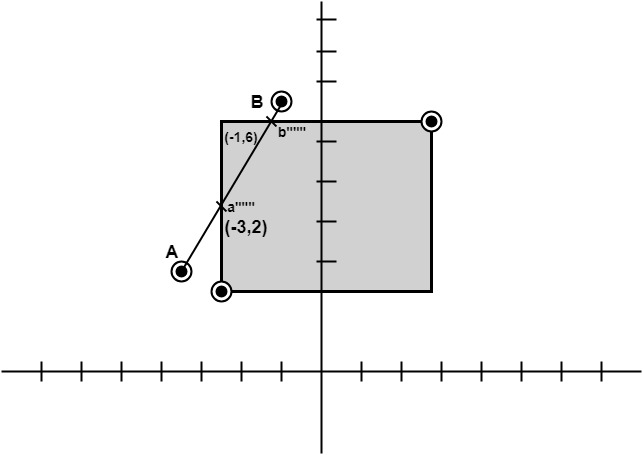
x5lie on point of intersection of boundary of window. Advantage of midpoint subdivision Line Clipping:It is suitable for machines in which multiplication and division operation is not possible. Because it can be performed by introducing clipping divides in hardware. Algorithm of midpoint subdivision Line Clipping:Step1: Calculate the position of both endpoints of the line Step2: Perform OR operation on both of these endpoints Step3: If the OR operation gives 0000 Step4: For the line to be clipped. Find midpoint Step5: Check each midpoint, whether it nearest to the boundary of a window or not. Step6: If the line is totally visible or totally rejected not found then repeat step 1 to 5. Step7: Stop algorithm. Example: Window size is (-3, 1) to (2, 6). A line AB is given having co-ordinates of A (-4, 2) and B (-1, 7). Does this line visible. Find the visible portion of the line using midpoint subdivision? Solution: Step1: Fix point A (-4, 2) 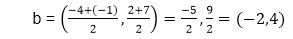 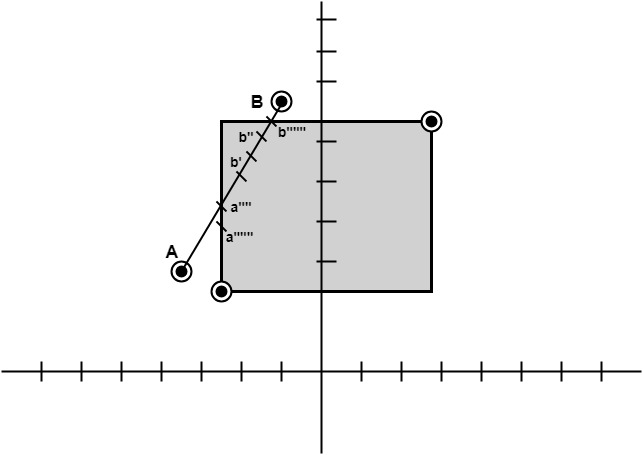
Step2: Find b"=mid of b'and b 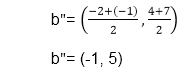
So (-1, 5) is better than (2, 4) 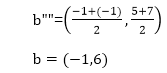
So B""to B length of line will be clipped from upper side Now considered left-hand side portion. A and B""are now endpoints Find mid of A and B"" A (-4, 2) B ""(-1, 6) 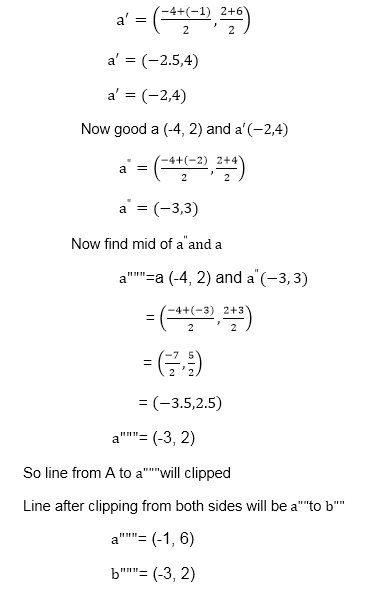
Liang-Barsky Line Clipping Algorithm:Liang and Barsky have established an algorithm that uses floating-point arithmetic but finds the appropriate endpoints with at most four computations. This algorithm uses the parametric equations for a line and solves four inequalities to find the range of the parameter for which the line is in the viewport. 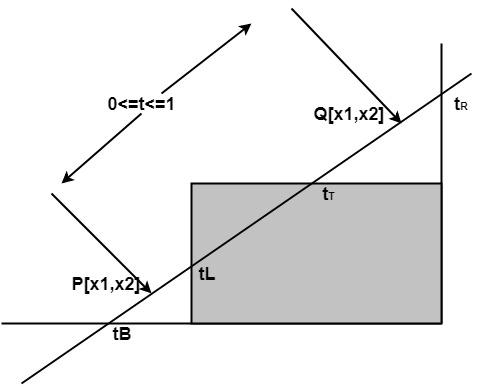
Let P(x1, y1), Q(x2, y2) is the line which we want to study. The parametric equation of the line segment from gives x-values and y-values for every point in terms of a parameter that ranges from 0 to 1. The equations are x=x1+(x2-x1 )*t=x1+dx*t and y=y1+(y2-y1 )*t=y1+dy*t We can see that when t = 0, the point computed is P(x1, y1); and when t = 1, the point computed is Q(x2, y2). Algorithm of Liang-Barsky Line Clipping:1. Set tmin=0 and tmax=1 2. Calculate the values tL,tR,tT and tB(tvalues). 3. If tmin< tmax? then draw a line from (x1 + dx*tmin, y1 + dy*tmin) to (x1 + dx*tmax?, y1 + dy*tmax? ) 4. If the line crosses over the window, you will see (x1 + dx*tmin, y1 + dy*tmin) and (x1 + dx*tmax? , y1 + dy*tmax?) are intersection between line and edge.
Next TopicText Clipping
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share









